Газета «Новости медицины и фармации» 6 (450) 2013

Математическая статистика — это наука, целью которой является разработка методов статистического наблюдения и анализ статистических данных, базирующаяся на понятиях и методах теории вероятностей.

Методы математической статистики (метаанализ) дают возможность объективно оценивать количественные результаты исследований, позволяют обрабатывать данные небольшого числа наблюдений, увеличивают достоверность заключений по материалам исследований. Математическая обработка результатов позволяет также в сжатой и четкой форме публиковать цифровые данные исследований вместо громоздких таблиц, занимающих много места и трудных для восприятия.

При проведении научных исследований, а также при изучении полученных цифровых результатов, как правило, приходится иметь дело с конечным определенным количеством данных. В этой ситуации необходимо на основании ограниченного числа исследований сделать те или иные обобщающие выводы.

Ошибки, допущенные при этом, могут привести к тому, что результаты того или иного исследования могут и не повториться, даже при соблюдении многих из тех условий, при которых они были получены.

Поэтому закономерно возникает вопрос: какое минимальное число исследований необходимо провести, чтобы могли проявиться закономерности, присущие изучаемому процессу (явлению)? На этот вопрос можно ответить следующее. Количество единиц наблюдения в каждом конкретном случае зависит от условий проводимого исследования, от его целей и задач. Признаки, на которые опирается исследователь для поиска или подтверждения интересующих его закономерностей, могут быть выявлены с различной степенью точности. Чем прочнее тот или иной признак присутствует в явлении, тем проще задача его выражения. Вполне очевидно, что для уяснения такого признака, при прочих равных условиях, требуется меньшее число исследований, чем при большей изменчивости.

Для изучения каждого такого явления важное значение имеет точность, с которой выносится данное суждение. Чем выше эта точность при одинаковых прочих условиях, тем оно убедительнее.

Для решения различных практических задач точность не обязательно должна быть одинаковой. В зависимости от сути исследования, а также условий, при которых оно проводится, в одних случаях точность может быть ниже, а в других — выше. Между точностью оценок суждения и степенью изменчивости исследуемых признаков существует определенное соотношение. Оно выражается в том, что количество необходимых исследований прямо пропорционально изменчивости признака и обратно пропорционально размеру ошибки, допускаемой при суждении.

Работая с цифровыми данными, то есть над количественной стороной результатов исследования, необходимо знать и правильно применять основные методы математической статистики, каждый из которых должен быть наиболее подходящим в каждом конкретном случае.

Чтобы получить необходимые статистические данные, требуется получить четкие и последовательные первичные результаты исследования, регистрируемые соответствующими документами (результаты экспериментов, анализы и пр.).

Для последующего статистического изучения результатов исследований необходимо определить объект исследования и единицу наблюдения. Только при точном определении единицы наблюдения и четком планировании исследования с ясно и четко поставленной задачей можно избежать неправильных обобщений и разного рода искажений действительности.

Недостаточно тщательные подбор и изучение качественной однородности сопоставляемых единиц наблюдения, как правило, приводят к недооценке и искажению действительно существующих различий в сравниваемых объектах наблюдения. Методы математической статистики не в состоянии компенсировать ошибки, обусловленные недостатками отбора и возможными качественными различиями отобранных единиц наблюдения. Как правило, наилучшие и самые значимые результаты достигаются при гармоничном сочетании тщательно проведенных исследований с наиболее рациональными методами математической статистики.

Вполне понятно, что полученные результаты исследования будут иметь научное и практическое значение, лишь когда можно будет с полной уверенностью ожидать, что при повторных исследованиях, проведенных в тех же условиях, в значительном большинстве случаев будет достигнут такой же результат, как в первом наблюдении. Чтобы быть уверенным в этом, необходимо знать, что выбраны правильные методики исследования и последующего статистического анализа.

В определенной мере достоверность среднего результата зависит от влияния случайностей. Известно, что ошибки в научной работе бывают систематическими и случайными. Систематические ошибки зависят, к примеру, от неправильной калибровки приборов, от недостаточной специфичности метода. В этих условиях результаты отличаются от истинных на более или менее постоянную величину, поэтому можно уменьшить погрешность путем введения специальных поправок, пересчетных коэффициентов и др.

Случайные ошибки возникают по самым разнообразным субъективным и объективным причинам. В отличие от систематических случайные ошибки могут при одном и том же виде изме­рений уменьшать или увеличивать результаты.

При налаживании и отработке методик исследования в конкретных условиях с использованием конкретных приборов, реактивов и материалов необходимо определять применительно к определенным задачам показатели чувствительности и точности методики. При измерении приборами, какими бы совершенными они ни были, никогда нет полной гарантии того, что при повторных измерениях результаты будут совершенно аналогичными. В связи с этим необходимо учитывать общую среднюю ошибку метода, полученную из ошибок всех этапов исследования, причем ее надо заранее рассчитать теоретически, а затем осуществлять контроль на практике. Определение ошибок отдельных этапов важно для выявления слабых мест той или иной методики, выработки приемов уменьшения ошибок отдельных этапов и, в конечном итоге, уменьшения общей средней ошибки метода.

Величина случайной ошибки характеризует точность метода, которая должна быть известна исследователю наряду с чувствительностью применяемого способа, так как иногда применяют методы, точность которых меньше значений, подлежащих изучению. Например, нельзя измерять вес (массу тела) лабораторных животных с точностью до 1 г на весах, точность которых s = ±10 г; нельзя изучать изменения концентрации холестерина в крови в сотых ммоль/л методом, ошибка которого равна ±0,1 ммоль/л.

Случайная погрешность метода характеризуется величиной ошибки измерения — средним квадратическим отклонением (s). В 68 % случаев погрешность метода не превышает значения s, а в 95 % случаев — 2s.

Определение ошибки измерения можно осуществить двумя способами.

Способ первый

Проводится 10 измерений, например, концентрация хлоридов плазмы одной и той же пробы крови у больных при аутоиммунном тиреоидите.

Получены следующие результаты. Хлориды плазмы крови (ммоль/л): 99, 100, 105, 102, 97, 100, 98, 103, 102, 95. М = 100. Отклонение каждого измерения от М (а): 1, 0, 5, 2, 3, 0, 2, 3, 2, 5. Квадрат отклонения (а²): 1, 0, 25, 4, 9, 0, 4, 9,25. Находим среднее арифметическое: М = 100 ммоль/л. Вычисляем отклонение (а) каждого измерения от М, не обращая внимания на знаки. Возводим отклонения в квадрат (а²) и находим сумму квадратов отклонения: ∑а² = 81.

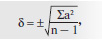
где n — число измерений.

Следовательно, величина ошибки одиночного определения хлоридов в плазме крови равна ±3 ммоль/л (при n > 30 из n не вычитают 1; при n ≤ 10 вычитание 1 считается обязательным).

Способ второй

Можно вычислить ошибку измерения — среднее квадратическое отклонение d в результатах параллельных измерений, проведенных у разных людей, или в эксперименте у лабораторных животных. Например, сделано 10 параллельных определений концентрации холестерина крови 10 больным вторичным гипотериозом. Получены следующие результаты. Холестерин крови (ммоль/л), первая серия: 6,8; 5,7; 8,3; 6,7; 5,2; 8,8; 7,2; 6,4; 4,5; 6,0. Холестерин крови (ммоль/л), вторая серия: 6,9; 5,6; 8,4; 6,5; 5,3; 8,6; 7,3; 6,4; 4,4; 6,2.

Находим отклонения (а) между результатами параллельных проб, не обращая внимания на знаки. Возводим отклонения в квадрат (а²) и находим сумму квадратов отклонений между результатами параллельных проб, равную 0,18.

Ошибка одиночного измерения (среднее квадратическое отклонение s) при данном способе ее определения равна ±0,1 ммоль/л.

При таком способе определения ошибки варьирования величин, измеряемых, к примеру, у различных людей или в эксперименте на лабораторных животных, не оказывают существенного влияния на результаты, так как при расчете учитывается лишь разница между результатами параллельных проб.

Можно повысить точность одиночных измерений путем осуществления нескольких параллельных измерений. В этом случае величина ошибки будет обратно пропорциональна значению квадратного корня из числа параллельных определений.

Знание величины ошибки измерения имеет значение для выбора метода исследования, оценки результатов и их записи. Общее правило при записи результатов измерения следующее: результаты измерений выражаются таким количеством знаков, которое отвечает точности измерения. При этом предпоследний знак должен быть точным, а последний — сомнительным.

Часто результаты измерений рассчитывают с излишней точностью. Например, показатели концентрации холестерина в крови определяют с точностью до сотых ммоль/л. Если ошибка измерения концентрации холестерина при применяемом методе равна ±0,1 ммоль/л, то и записывать результаты необходимо с точностью до десятых ммоль/л, округляя последующие цифры до десятых ммоль/л. При округлении следуют следующему правилу. При цифрах следующего разряда от 1 до 4 их просто отбрасывают, а при цифрах от 6 до 9 — отбрасывают, но прибавляют 1 к цифре предыдущего ряда. При цифре 5 прибавляют 1 к цифре предыдущего ряда, если она нечетная, и ничего не прибавляют, если она четная. Пример: 7,65; 7,75; 7,58; 7,43 ммоль/л округляем и получаем 7,6; 7,8; 7,6; 7,4 ммоль/л.

Средние величины. Общие положения

Средние величины в медико­биологических исследованиях имеют существенное значение, когда необходимо по какому­либо количественному признаку получить обобщенную характеристику явлений или процессов.

Средняя величина может служить общей характеристикой явления или процесса при обязательном условии, что отдельные количественные значения относятся к одному виду, то есть составляют количественно однородную совокупность. Например, это могут быть показатели холестерина крови, частота пульса, уровень артериального давления крови и др. у лиц одного пола, одной возрастной группы и сопоставимых по другим признакам.

Средние величины следует использовать в научной работе при изучении данных, сгруппированных по наиболее типичным для изучаемых явлений и процессов признакам.

Возможные ошибки при использовании средних величин имеют место, когда средние величины представляют изучаемые явления и процесс в общем виде, без детального распределения на качественно однородные группы. Метод группировок является основой научного использования метода средних величин.

В условиях эксперимента, при проведении тех или иных опытов для получения сравнимых данных, все составляющие элементы достаточно однородны. По ходу опыта исследователь при необходимости может изменить условия эксперимента. Средние величины, полученные в результате данного эксперимента, определяются теми условиями, в которых осуществляются проводимые опыты.

В научных медицинских работах иногда встречаются различия проводимых средних величин по одному и тому же явлению (процессу), что в известной мере объясняется недостаточным вниманием к соответствующей группировке данных. В итоге сравнению подлежат качественно неоднородные группы. В соответствии с этим получают несопоставимые результаты.

Средние величины в сочетании с группировкой четко выделяют типичные признаки, которые характеризуют изучаемые явления и процессы.

Средняя арифметическая величина. Методика определения

Средней арифметической простой называется частное от деления суммы отдельных вариант на их число. Средняя величина обозначается М, x, у и так далее.

Пример

В эксперименте у лабораторных животных (кроликов­самцов породы шиншилла, масса тела 2,5 ± 0,2 кг) изучали содержание глюкозы в крови при экспериментальном аллоксановом диабете. Получены данные: 7,1; 8,1; 5,2; 8,6; 7,0; 8,1; 9,1; 6,6; 8,1; 8,6; 8,1 ммоль/л. Средняя величина М = 7,69 ммоль/л. При этом наименьшая величина в образце равна 5,2, а наибольшая составила 9,1 ммоль/л. Разброс колебаний: 9,1 – 5,2 = 3,9. Анализ приводимых данных нельзя ограничить этими цифрами. Однако в некоторых исследованиях числовая обработка величин, измеряющих сравниваемые явления, заканчиваются определением средней величины и амплитуды ряда (от и до). Ряды распределения с большим числом наблюдений, как правило, фиксируют в сгруппированном виде.

Нельзя ограничить анализ приводимых данных только определением средней арифметической величины и амплитудой ряда, так как этим не ограничивается числовая обработка ве­личин, измеряющих сравниваемые ­явления.

Средняя арифметическая взвешенная характеризует частоту каждого интервала, которая показывает, сколько раз повторяется варианта в каждой группе. Для получения средней арифметической взвешенной следует умножить середину интервала каждой группы на соответствующие частоты, произведения суммировать и сумму произведений разделить на число наблюдений.

Получаемые средние величины являются мерой сравнения и оценки изучаемых явлений и процессов. Однако средняя арифметическая величина, взятая сама по себе, иногда имеет ограниченное значение, так как не отражает размеров изменчивости (колебаний) количественных вариант ряда.

Научную и практическую значимость имеют не только числовые значения средних величин как таковых, но и в значительной мере изменчивость отдельных показателей и их соотношения друг с другом. Возможна ситуация, когда сравниваемые явления характеризуются средними одной и той же величины, однако числовые соотношения между отдельными вариантами, равно как и амплитуды сравниваемых рядов, оказываются различными.

Амплитуда ряда, то есть разность между наибольшей и наименьшей вариантами, определяет колебание показателей изучаемого ряда. К недостаткам значимости амплитуды ряда как критерия колебания следует отнести тот факт, что она определяет только величину абсолютной разности двух крайних количественных показателей ряда и не учитывает соотношений между промежуточными вариантами внутри самого ряда. Однако расположение вариант между собой внутри ряда может значительно варьировать.

Амплитуда ряда не является надежной мерой изменчивости, потому что значительно изменяется в зависимости от числа наблюдений.

Мера колебания ряда распределения представляет одну из значимых характеристик, необходимых при анализе показателей.

Значимость применения методов математической статистики в медико­биологических исследованиях состоит в оценке достоверности различий между отдельными сериями наблюдений или между теоретическими и экспериментальными данными. Успешное решение этой задачи позволяет ответить на вопрос, являются ли получен­ные различия случайными или они ­обусловлены какими­то определенными причинами.

Применение математических критериев различия производится в следующем порядке. Вначале предполагаем, что исследуемые явления идентичны по данному признаку, а имеющиеся различия объясняются случайным характером выборок. Такое предположение называется нулевой гипотезой. На основании нулевой гипотезы определяют значения некоторых числовых характеристик, параметры распределения которых известны из теоретических соображений. Если вероятность появления этих значений невелика (менее 5 %, а в отдельных случаях — менее 1 % или даже 0,1 %), нулевая гипотеза отвергается и делается вывод о существенной значимости имеющихся различий. В противном случае эти различия считают недостаточно существенными.

При исследовании одной выборки могут представлять интерес вопросы о принадлежности всех вариант к одной и той же генеральной совокупности и о соответствии полученных данных какому­либо теоретическому закону распределения. Ответом на этот вопрос может служить правило трех сигм и критерий грубых ошибок наблюдения.

При сопоставлении двух или нескольких выборок при помощи математических критериев различия можно определить наличие или отсутствие различий по данному признаку у соответствующих генеральных совокупностей, а также наличие или отсутствие связи между двумя признаками.

Применяемые критерии различия делятся на параметрические и непараметрические. Параметрические критерии основываются на предположении о наличии нормального или близкого к нему закона распределения вариант и связаны с вычислением выборочных средних и выборочных дисперсий. Непараметрические критерии различия не зависят от вида распределения, не связаны с вычислением моментов распределения и одинаково пригодны как для количественных, так и для качественных показателей.

Средняя арифметическая величина М сама по себе не может дать достаточно полную характеристику того или иного показателя, так как не позволяет оценить степень варьирования измеренных величин. Четкое представление о тех или иных показателях дает средняя арифметическая величина М в сочетании со средним квадратическим отклонением (стандартное отклонение), которое обозначается греческой буквой s (сигма).

Среднее квадратическое отклонение s характеризует величину случайной погрешности (уровень колебания) результатов исследования.

При количестве исследований более 30 среднее квадратическое отклонение вычисляют по формуле:

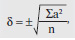
где а² — квадрат отклонений каждой величины от средней величины М, ∑ — знак суммы, n — количество наблюдений.

При небольшом количестве наблюдений (менее 30) вычисление среднего квадратического отклонения проводят по формуле:

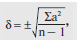
где ∑ — знак суммы, а² — квадрат отклонения каждой измеренной величины от средней М, n — количество исследований (при n менее 30 вычитание 1 считается обязательным).

Принадлежность варианты к совокупности. Правило трех сигм

При определении принадлежности варианты к совокупности наиболее простым критерием является правило трех сигм. Согласно этому правилу, варианта x считается принадлежащей к совокупности, если она отличается от выборочного среднего М не более чем на три средних квадратических отклонения, то есть:

[х – М] ≤ 3σ.

При несоблюдении этого условия рассматриваемая варианта считается анормальной и исключается из выборки.

Пример

При изучении содержания и уровня холестерина в крови у больных гипотиреозом были получены следующие результаты: 3,8; 4,6; 5,1; 4,2; 3,9; 4,4; 5,3; 7,8; 4,7; 4,5; 4,1; 5,2 ммоль/л. Необходимо определить, являются ли некоторые из полученных значений анормальными вследствие грубых ошибок или особых условий наблюдений. Находим выборочное среднее и среднее квадратическое отклонение результатов измерений: x = 4,80 ммоль/л, а = 0,995 ммоль/л. Проверяем выполнение условия трех сигм для наибольшего значения (в данном случае это 7,8 ммоль/л). Так как условие в данном случае не выполнено, показатель необходимо исключить из выборки.

Среднее квадратическое отклонение s как мера изменчивости имеет преимущество в том, что эта величина дает возможность проверки существующих различий сравниваемых явлений и процессов в виде оценки точности и надежности полученных результатов.

Среднее квадратическое отклонение s как меру изменчивости при большом числе наблюдений, как правило, вычисляют в сгруппированных рядах, обычно применяя упрощенные способы вычисления, которые приведены далее в тексте. Если число наблюдений менее 100, то полученную величину среднего квадратического отклонения s надо умножить на:  где n — число наблюдений; такой же результат будет получен, если средний квадрат отклонений разделим заранее на число наблюдений без одного (n – 1). Эту поправку в величине среднего квадратического отклонения необходимо внести, если в дальнейшем нужно оценить точность и надежность результатов в связи с малым числом наблюдений.

Коэффициент изменчивости (вариации)

Среднее квадратическое отклонение s является именованным числом, то есть обозначается в тех же конкретных единицах измерения, что и средние числа. Когда абсолютные меры изменчивости, например частота пульса, систолическое и диастолическое артериальное давление и другие, не дают возможности сравнивать их между собой, применяются относительные числа изменчивости (уровень колебания), то есть отвлеченные, а не именованные числа. При определении относительной меры изменчивости учитывают отношение среднего квадратического отклонения s к средней величине М, умноженное на 100. Данная величина определяется как коэффициент изменчивости С и представляет собой отношение среднего квадратического отклонения к средней величине, выраженное в процентах. Коэффициент изменчивости (вариации):

Определение коэффициента изменчивости представляет интерес и может быть полезным при сравнении нескольких явлений. Относительные числа изменчивости в виде коэффициента вариации С четко и правильно показывают истинные соотношения изучаемых показателей.

При изучении медико­биологических исследований возникает необходимость дать объективную оценку реальности и степени достоверности полученных результатов. Ошибки разных измерений уравнивают друг друга, и это позволяет уменьшить значение отдельных ошибок при сравнении результатов исследований. Имеется очень малая вероятность того, что при повторных измерениях ошибки всегда будут направлены в одну сторону. Влияние ошибок отдельных измерений на результаты уменьшается при увеличении числа измерений.

При изучении достоверности результатов ряда исследований пользуются не ошибками одиночного измерения, а ошибкой средней арифметической величины (средняя ошибка, средняя квадратическая ошибка), обозначаемой буквой m. Значение m уменьшается пропорционально квадратному корню из числа наблюдений. Вычисление m проводят по формуле:

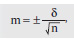
где s — среднее квадратическое отклонение, n — число измерений.

В тех случаях, когда количество измерений менее 30, при вычислении средней ошибки вместо n принимается n – 1, то есть число исследований уменьшают на единицу. В этой ситуации вычисление проводят по формуле:

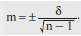
Практическое значение средней ошибки m заключается в том, что она дает возможность определить достоверность средних и относительных величин, степень их отклонения в выборочном исследовании от аналогичных результатов, которые могли быть получены, если бы исследование было сплошным.

Теория математической статистики доказывает, что путем прибавления и вычитания одной средней ошибки m из средней арифметической величины М можно определить размер отклонения этих величин по выборке от их величины, которая могла быть получена при сплошном исследовании (генеральная совокупность). Однако прибавление или вычитание из средней величины М одной ее средней ошибки m не дает полной гарантии, что при повторных исследованиях в аналогичных условиях полученный результат будет всегда находиться в этих пределах.

Известно, что при М ± m результат повторного аналогичного исследования в 68,3 % случаев будет в этих пределах, а в 31,7 % — может находиться за этими пределами. Такая гарантия в математической статистике считается недостаточной. Рекомендуется определять пределы возможных колебаний показателей путем прибавления и вычитания двух средних ошибок средней арифметической величины М ± 2m.

В некоторых случаях, когда по условиям исследования нужна еще более высокая гарантия, при расчетах среднюю ошибку m утраивают. При этом условии в 99,7 % случаев гарантируется, что результат повторного исследования попадет в границы доверительного интервала М ± 3m (средняя арифметическая величина ± ее утроенная средняя ошибка). Утроенная средняя ошибка средней арифметической величины называется максимальной ошибкой.

При статистическом анализе существенное значение имеет определение достоверности разности сравниваемых относительных и средних величин. Математическая статистика располагает возможностью объективной оценки достоверности различия сравниваемых показателей.

Для решения вопроса о случайности и неслучайности расхождения наблюдаемых средних (относительных) величин поступают следующим образом. Необходимо определить среднюю ошибку разности двух сравниваемых средних величин. Средняя ошибка разности сравниваемых величин может быть вычислена по формуле:

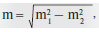
где m₁ — средняя ошибка одной сравниваемой средней, m₂ — средняя ошибка другой средней арифметической величины.

Полученная таким образом средняя ошибка разности сравнивается с величиной этой разности. Для достоверности разности двух показателей, как и для достоверности отдельных показателей, необходимо, чтобы эта разность превышала свою ошибку в число раз, определяемое доверительным коэффициентом t.

Доверительный коэффициент t показывает, во сколько раз разность между сравниваемыми средними величинами больше значения квадратного корня из суммы их средних ошибок. Вычисление достоверности разности двух показателей проводят по формуле:

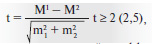
где t — доверительный коэффициент, М¹ – М² — разность двух средних величин,  — ошибка этой разности.

Если соотношение разности сравниваемых средних величин к ошибке разности менее 2,5, то расхождение между средними величинами можно считать недоказанным. Если соотношение более 2,5, то его следует считать неслучайным. При достаточно большом количестве исследований (более 30) вместо t = 2,5 можно, согласно этому правилу, использовать t = 2.

В биологических и медицинских исследованиях значительное распространение получил способ обработки результатов при небольшом количестве исследований (менее 30) при помощи таблиц t, предложенных Стьюдентом. Этот способ позволяет вычислить степень достоверности различий при небольшом числе измерений по данным значений М, s, m, n. Между коэффициентом t и вероятностью возможной ошибки р существует определенная взаимосвязь. Чем выше доверительный коэффициент t, тем меньше вероятность ошибки р при оценке результатов исследования. По таблице t определяют вероятность возможной ошибки в оценке результатов исследования.

В медико­биологических исследованиях принято считать различие достоверным (значимым) начиная со значения р < 0,05, то есть когда вероятность различия больше 95 % шансов из 100, а против — меньше 5 шансов. При р < 0,01 вероятность различия больше 99 %, а при р < 0,001 — больше 99,9 %, то есть за правильность вывода 999 шансов из 1000, а против — только 1 шанс.

Современные методы математической статистики при обработке малого числа наблюдений дают четкое представление о результатах, которые следует ожидать при бесконечном повторении опытов.

Следует отметить некоторую условность общепринятого критерия достоверности, когда различие достоверно только при р < 0,05, а по мнению некоторых авторов — даже при р < 0,001. Очевидно, что оценка значений вероятности различия должна основываться на реальных условиях, то есть в каждом конкретном случае при суждении о результатах, кроме значения р, необходимо учитывать биологические и медицинские особенности, связанные с изучаемым вопросом. С учетом всего изложенного считаем необходимым снова подчеркнуть значение р как показателя достоверности различия. Например, при р < 0,001 уверенность в правильности выводов будет выше, чем при р < 0,01 и тем более при р < 0,05.

В научной работе при определении достоверности различия возможны следующие типичные варианты:

- определение достоверности количественных различий результатов исследований, проведенных на различных группах больных или в эксперименте на подопытных животных;

- определение достоверности количественных различий результатов исследований, проведенных в динамике на одной группе;

- определение достоверности различий при альтернативном варьировании, когда делают заключение о различии по качественным изменениям признака.

Вариант 1

Определение достоверности различий результатов исследований, проведенных на различных группах. Вначале нужно рассчитать значения средних арифметических величин М для каждой группы. Затем на основе М вычисляют величины квадратических отклонений s для каждой группы по формуле:

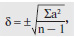
где ∑a² — сумма квадратов отклонений каждой измеренной величины от М, n — число опытов.

Из значений s и n вычисляют среднюю ошибку m по формуле:

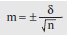
По данным М и n определяют показатель существенности разницы (t). На основании величины t и числа наблюдений по таблице t определяют вероятность различия р. При использовании таблицы из числа наблюдений (n) вычисляют значение степени свободы (n ). При сравнении двух рядов:

n' = n₁ + n₂ – 2,

где n₁ и n₂ — числа вариантов в рядах.

Вариант 2

Определение достоверности различий результатов исследований, проведенных в динамике на одной группе. В данном случае вычисления вероятности различия основываются на разнице определений. Применение разностного метода позволяет четко проводить определение вероятности различия, так как варьирование показателей в каждом ряду не оказывает такого влияния, как при непосредственном сравнении средних арифметических величин и средних ошибок.

Применение разностного метода обработки результатов наблюдений не исключает возможность применения первого варианта (непосредственное сравнение средних арифметических значений и средних ошибок) в случае незначительного варьирования показателей в пределах ряда наблюдений. Вариант 1 предпочтителен при необходимости определения достоверности различий двух групп. При обработке результатов определений в динамике одной группы более приемлем вариант 2. Выбор способа обработки результатов в каждом конкретном случае зависит от особенностей исследования и характера результатов исследования.

Вариант 3

Определение достоверности различий при альтернативном варьировании. Здесь математическая обработка результатов исследования дает возможность получить дополнительную, нередко довольно обширную информацию и раскрыть внутреннее содержание результатов экспериментов.

В математической статистике разработаны методы, позволяющие проводить обработку результатов исследований с помощью приемов, дающих так называемые эффективные оценки. Важным фактором здесь является то, что оценку параметров и установление доверительных интервалов для них производят некоторым стандартным образом. Это обстоятельство дает различным исследователям возможность получать сопоставимые результаты. Имеется возможность оценивать, анализировать и обобщать научные работы, выполненные с использованием стандартных критериев оценки изучаемых параметров.

Методы математической статистики, в частности статистическая обработка результатов исследований, используются не всегда правильно и достаточно эффективно. Пренебрежение стандартными формами представления материала приводит к значительным изъянам в исследованиях. Иногда возникают искажения вследствие использования логически не осмысленных и математически не обоснованных показателей в оценке результатов. Поэтому результаты работ, проведенных различными авторами, не только иногда оказываются несопоставимыми, но при этом возникают ошибки и кажущиеся противоречия. В ряде научных работ встречаются различные ошибки при статистической обработке материала. Так, иногда авторы в научной работе приводят значения только средней арифметической величины М и средней ошибки m, а показатели t и р, характеризующие критерий достоверности, не приводят (и, по­видимому, не рассчитывают, так как в тексте на них нет ссылок). В тех же случаях, когда названные показатели рассчитаны, это бывает сделано не всегда правильно. Не имеют смысла также ссылки на формулы, не подкрепленные соответствующими расчетами. В некоторых научных работах их авторы в погоне за кажущейся экономией времени без учета предъявляемых требований, в том числе степени точности критериев значимости, используют различные упрощенные способы математической обработки данных. Однако эти методы можно применять только в тех случаях, когда их мощность (степень точности) соответствует заданному уровню значимости. Вместе с тем редко используются критерий Фишера (Fisher R.A.), вычисление коэффициента корреляции, методы многофакторного дисперсионного анализа и др.