Газета «Новости медицины и фармации» №6 (691), 2019
Вернуться к номеру
Мышление как объект математического моделирования
Авторы: Теленгатор А.Я., Кондратенко В.А.
Киевский медицинский университет, г. Киев, Украина
Рубрики: Неврология
Версия для печати
Будущий врач, как мы полагаем, должен представлять себе сущность модели мышления человека. В медицинских университетах и институтах обычно на лекциях и практических занятиях этим вопросам уделяется мало времени либо они вообще не рассматриваются. В то же время тайна феномена «мышление человека» вызывает интерес у исследователей, врачей и вообще у многих людей. Не только физиологи размышляют над законами, которым подчиняется мышление человека. Математики эти законы определили и пользуются ими [1], к сожалению, не так активно, как следовало бы для успешного решения насущных задач в любой из множества областей человеческой деятельности. Пассивность в применении возможностей математики, например в медицине, связана с доминирующим численным моделированием математиками предметных задач в этой области человеческой деятельности, а также с неосведомленностью медиков о возможностях моделирования процессов мышления средствами математической логики, возможностями аксиоматического моделирования [2, 3]. Трудно переоценить преимущества теории аксиоматического моделирования перед ставшим традиционным численным моделированием, так как в ее основе лежат естественные законы мышления человека, выраженные в математических формулах. Поисками законов мышления, изучением реализующих его процессов заняты и врачи-неврологи [4–7], так как глубокое понимание природы той или иной патологии, затрагивающей процессы мышления, неизбежно приводит к мысли о возможности и необходимости математического моделирования самого процесса мышления для прогноза и лечения заболеваний. Процесс такого моделирования достаточно сложный и малоизученный. Предложенная физическая модель мышления [2, 8] опирается на учение о рефлекторных кольцах [9] и функциональных системах [10], что позволяет легко описать этот процесс в терминах аксиоматической модели. Для этой цели необходимо определить базовые знания, аксиомы, которые позволят описать процесс мышления человека [6]. Цель настоящей работы — рассмотреть мышление как объект математического моделирования.
Стало понятным, что психика конкретного человека по типовому проекту его генома в нейронных сетях –нервной системы формирует для каждой мысли отдельное рефлекторное кольцо на основе кодовых слов во второй сигнальной системе, которыми идентифицируются физические величины в рефлекторных кольцах первой сигнальной системы.
Мысль считается элементарной и корректной, если она выражается одним кодовым словом, которому соответствует одна физическая величина в отдельном рефлекторном кольце первой сигнальной системы.
Мысль считается составной и корректной, если она выражается несколькими кодовыми словами, каждому из которых соответствует одна физическая величина в отдельном рефлекторном кольце первой сигнальной системы.
Каждому конкретному человеку неизвестны те ограничения, которые зафиксированы в его геноме, а именно в правилах работы второй сигнальной системы. В частности, ограничение, не допускающее присутствия во второй сигнальной системе кодовых слов, не имеющих физической реализации в формате рефлекторного кольца первой сигнальной системы.
За этим ограничением стоит нецелесообразность использования конкретным человеком нематериализованных мыслей, называемых гипотетическими. Использование гипотетических мыслей в живой материи (например, в вегетативной нервной системе человека) недопустимо, так как неизбежно ведет к катастрофе в жизнедеятельности этой материи.
Для научной деятельности, в точных науках, например, эти правила сформулированы в специальной науке, называемой математической логикой. Целью познания точных наук является исключительно логика причинно-следственных отношений между физическими переменными величинами, функционально полно характеризующими все без исключения состояния динамических систем произвольной сложности [3]. Математическая логика — это функционально полный формальный язык, специально предназначенный для афористического (максимально возможной краткости и точности) стиля описания логической сущности исследуемых процессов и явлений в мироздании.
Качественные характеристики мышления таковы [7]. Мышление возникает на основе практической деятельности, из чувственного познания, но выходит далеко за его пределы. В свою очередь, правильность мышления проверяется в ходе практики.
На уровне второй сигнальной системы воспринимаются слова, и приходящие сюда сигналы заменяются речью. Поэтому мышление неразрывно связано с речью, как внутренней, так и внешней. Мышление формирует понятия, их понимание, а также их взаимосвязи. Мышление оперирует понятиями, которые по своей форме являются словами, а по сути — результатом мыслительных операций. В свою очередь, в результате мышления может происходить уточнение словесных понятий.
Мышление имеет место только тогда, когда имеется проблемная ситуация. Если же можно обойтись старыми способами действия, то мышление не требуется.
Основные виды мышления
По мере развития психики человека в процессе его социализации мышление последовательно проходит четыре стадии.
Первый способ мышления ребенка — предметно-действенное мышление (в возрасте от 1 до 3 лет), то есть мышление в виде практических действий. Маленькие дети познают окружающий мир и делают первые выводы о его устройстве, пробуя предметы руками, разбирая их и ломая.
Следующая ступень — наглядно-образное мышление, в виде наглядных образов и представлений (зрительных, слуховых, тактильных). Оно наиболее развито в возрасте от 4 до 7 лет, но сохраняется и у взрослых людей. Это мышление опирается на практическую реальность, но уже может создавать и хранить образы, не имеющие прямого аналога в ощущениях (сказочные персонажи).
В образном мышлении, которое наиболее развито у художников, дизайнеров, рекламистов, портных, парикмахеров, архитекторов, материалом для решения задачи являются не понятия, а образы — чаще зрительные (у музыкантов — слуховые). Они либо извлекаются из памяти, либо воссоздаются воображением. Отличием от предыдущего этапа является широкое использование словесных конструкций в формировании и преобразовании образов, а также использование отвлеченных понятий.
Абстрактно-логическое (отвлеченное или понятийное) мышление работает в форме отвлеченных понятий, символов и цифр. В этом случае человек оперирует понятиями, не имея дела с опытом, полученным при помощи органов чувств.
Например, термины этики — «справедливость» и «совесть»; математические термины — «степень» и «производная»; экономические термины — «баланс» или «прибыль» являются абстрактными понятиями и не могут восприниматься непосредственно органами чувств человека.
Формы мышления
Основными формами мышления [11] являются понятия, суждения и умозаключения.
Понятие — мысль, в которой отражаются общие, существенные признаки предметов и явлений.
Например, в понятие «человек» входят такие существенные признаки, как трудовая деятельность, прямохождение, членораздельная речь и т.д. Отличие понятия от представления состоит в том, что представление — это всегда образ, а понятие — это мысль, выраженная в слове. Кроме того, представление включает в себя как существенные, так и несущественные признаки, а понятие — только существенные. Содержание понятий раскрывается в суждениях.
Суждение — это отражение связей между предметами и явлениями или между их свойствами и признаками.
Из двух или более суждений можно построить следующую по сложности форму мышления — умозаключение.
Умозаключение — такая связь между понятиями или суждениями, в результате которой из одного или нескольких суждений мы получаем новое суждение.
Мыслительные операции
Процесс мышления включает в себя несколько операций: сравнение, анализ, синтез, абстракция, обоб–щение, конкретизация.
Анализ — мысленное расчленение объекта на составляющие его элементы с последующим их сравнением. Например, психолог проводит анализ личностных качеств своего клиента на основании результатов теста.
Синтез — объединение отдельных компонентов в целое. Обычно соседствует с анализом. Продолжая предыдущий пример, представим себе, как психолог после анализа нескольких тестов строит обобщенный психологический портрет человека.
Абстрагирование — выделение одной стороны предмета или явления, которая в реальности как отдельная не существует. В результате абстракции формируются понятия. В качестве примера можно взять понятие «надежность» как низкую вероятность поломки какой-нибудь разновидности бытовых приборов.
Обобщение — выделение общих существенных свойств в сравниваемых объектах.
Сравнение — это сопоставление предметов и явлений с целью нахождения сходства и различия между ними.
Например, произведя анализ продаж отдельных сортов хлеба, хозяин пекарни приходит к выводу, что наилучшим спросом пользуются сдобные булочки, независимо от их размеров и начинок.
Конкретизация — операция, обратная обобщению, выделение у предмета или явления характерных именно для него черт, не связанных с чертами, общими для класса предмета или явления. Например, хозяин мини-пекарни, обнаружив повышенный спрос на сдобные булочки, решает выпекать их новый вид — с кунжутом и клубничной начинкой.
Эти сведения легко могут быть описаны в терминах математической логики и сформулированы в виде аксиом для решения задач аксиоматического моделирования. Математическая логика — это функционально полный формальный язык, специально предназначенный для афористического (максимально возможной краткости и точности) стиля описания логической сущности исследуемых процессов и явлений в мироздании.
Сущность мышления изучена плохо. Все, что мы знаем наверняка о механизмах мышления, — это то, что сам процесс представляет собой сложную аналитико-синтетическую деятельность головного мозга. В осуществлении процессов мышления принимает участие весь головной мозг, образуя сложные временные связи между отдельными мозговыми структурами. В осуществлении процесса мышления принимают участие нервные процессы в речевых центрах коры. Мышление опирается не только на первосигнальные связи. Оно обязательно предполагает деятельность второй сигнальной системы в ее неразрывной связи с первой сигнальной системой. Раздражителями здесь выступают уже не конкретные предметы окружающего мира и их свойства, а слова. Речь, будучи непосредственно связанной с мышлением, позволяет отразить в словах взаимосвязь и взаимообусловленность явлений, потому что слова являются не просто заместителями, сигналами предметов, а обобщенными раздражителями. Интегрированная сенсорная картина события передается лобной коре. Благодаря обширным двусторонним связям с лимбической системой к этой картине добавляется эмоциональный оттенок, а также информация, взятая из памяти. Другие нервные связи тоже доставляют информацию, которая позволяет лобной коре оценить текущие требования организма и окружающей среды и выбрать среди них первоочередные — решить, что лучше, а что хуже для организма в данной ситуации. Лобная кора, по-видимому, ответственна и за выбор целей, которые мы ставим перед собой на будущее, а также за нашу оценку различных обстоятельств в связи с этими целями. Но каждое полушарие — левое и правое — имеет свою собственную отдельную цепь воспоминаний и усвоенных знаний, недоступных для другого. Во многих отношениях каждое из них имеет как бы отдельное собственное мышление. Где именно в коре происходят эти сложнейшие процессы фильтрации и абстрагирования данных и как они осуществляются, пока неизвестно. Однако, как показали современные методы исследования, большая часть того, что прежде называли «ассоциативной корой», возможно, состоит из ряда сенсорных зон все более высокого порядка, наивысшая из которых получает, фильтрует и интегрирует информацию от различных органов чувств. Основной тип строения коры — это вертикальные колонковидные образования, состоящие примерно из 100 клеток. Особая роль этих кортикальных колонок в «ассоциативных» полях, а также во всей коре, вероятно, связана с их способностью к установлению ассоциаций, т.е. образованию временных связей с другими колонками из других участков мозга. При изменении условий такие связи могут изменяться. Более того, кора во всякое время располагает как информацией внутреннего происхождения (повторной), так и текущей информацией о внешнем мире. Этот непрерывный пересмотр воспринимаемых образов наряду с функциями сравнения или тестирования реальности позволяет коре объединить образ, сформированный в ближайшем прошлом, с текущим образом внешнего мира. Сравнение внутренних показаний с текущей информацией об окружающем мире и составляет предполагаемую основу сознания. В настоящее время ученые пытаются найти способы проверки этой фундаментальной концепции. Известно также, что наш мозг и анатомически, и физиологически, по-видимому, от рождения подготовлен к переработке словесных сигналов. У большинства из нас частью мозга, которая запрограммирована для этой функции, является кора левого полушария. В отличие от большинства сенсорных и двигательных функций процесс становления речевой функции обладает значительной пластичностью. Например, при повреждении речевых областей коры левого полушария в ранний период жизни выполнение их функций берут на себя корковые зоны правого полушария. Сегодня мы имеем уникальную возможность максимально кратко в математической терминологии описать полученные исследователями знания. Эту возможность предоставляет раздел классической математики — логика предикатов. Так как в процессе познания материи выявляется исключительно логика ее жизнедеятельности, получившая статус естественных законов жизнедеятельности неживой и живой материи, то наиболее подходящей математической структурой для оперирования логическими функциями является логика предикатов первого порядка. Ее непревзойденным преимуществом является тот факт, что работает она:
1) непосредственно с мыслями человека, предварительно нагруженными оценками экспертов, с точки зрения их «истинности» или «ложности» (такие мысли называются операндами);
2) с четырьмя логическими операциями («конъюнкция», «дизъюнкция», «отрицание», «импликация»):
— операция конъюнкции ˄ несет смысловую нагрузку интегрирования истинных элементарных смыслов в обобщенный истинный смысл;
— операция дизъюнкции ˅ несет смысловую нагрузку представления для выбора одного из альтернативных смыслов, который должен быть непременно истинным, чтобы весь составной операнд можно было считать истинным;
— операция импликации → несет такую смысловую нагрузку: если составной операнд посылки и составной операнд заключения истинны, то и формула в целом истинна;
— операция отрицания not несет смысловую нагрузку противоположной экспертной оценки: отрицание истины — это ложь, отрицание лжи — истинно.
Синтаксис языка логики предикатов определяется с помощью следующих четырех правил:
1. Операндами в алфавите являются высказывания, утвердительные предложения, о которых можно сказать, истинны они или ложны.
2. Атомы — неделимые исходные высказывания. Атом есть формула.
3. Если F и G — формулы, то not(F), (F ˅ G), (F ˄ G), (F → G), (F ≡ G) тоже формулы.
4. Если F(X) — формула, а X — предметная переменная, то (X)F(X) и (X)F(X) тоже формулы.
Формулы порождаются только конечным числом применения правил 1–3.
Аксиома — это высказывание, проверенное многократно и убедившее всех в своей истинности.
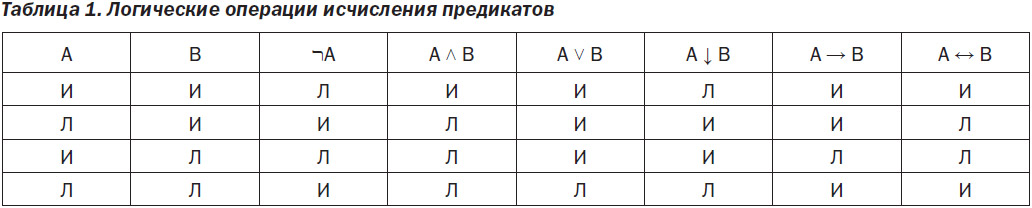
По определению атом может иметь только два значения: либо «истина» (И), либо «ложь» (Л). Каждое из этих значений называется истинностным. Правила присвоения истинностных значений формулам на основе исходных значений атомов приводятся в табл. 1. Других правил не существует.
Логика предикатов первого порядка обладает функциональной полнотой.
Это означает:
— во-первых, что не существует мыслей или смыслов, которые не могут быть корректно структурированы с помощью упомянутых четырех логических операций в архитектуре мыслей любой сложности;
— во-вторых, что любые архитектуры мыслей, связанные корректно логической операцией импликации, могут с абсолютной достоверностью рассматриваться как теоремы по тематике любых естественных, гуманитарных и прикладных наук;
— в-третьих, упомянутые теоремы могут быть непременно доказаны с точки зрения их истинности или ложности с помощью простейшего формального алгоритма, вручную или автоматически;
— в-четвертых, эта логика покрывает в том числе и отношения физических величин, выраженных в численных значениях (численные выражения любой сложности), оценивая их предварительно с точки зрения их истинности («истина» или «ложь»); например, любой из законов Ньютона или Галилея или любая из химических формул или им подобных законов.
Предикаты в логике предикатов первого порядка являются логическими функциями с известными заранее значениями («истина» или «ложь») и нагружаются как элементарными мыслями, так и мыслями любой архитектурной сложности. За истинность исходных мыслей ответственность возлагается на постановщиков логических задач. Логика предикатов первого порядка — это математическая структура, кардинально решающая проблему общения научных работников в естественных науках и обеспечивающая повышение эффективности решения в аналитическом формате проблемных задач познания мироздания радикально и без компьютерной поддержки.
Ключевое понятие в логике предикатов — предикат. Определение понятия предикат — это логическая функция одной или многих абстрактных переменных X1, X2, …, Xn, принимающая одно из двух допустимых значений («истина» или «ложь») при одновременной замене абстрактных переменных их конкретными смысловыми значениями. Имеет формульный вид: p(X1, X2, …, Xn), в котором предикатный символ p несет на себе смысловую нагрузку передачи сущности тех отношений или операций между абстрактными переменными, которые исследователь реального мира хочет отобразить в этой формуле. Любая формула тоже может быть представлена в виде предиката. Сущность отношений и операций ограничений не имеет и определяется фантазией исследователя. Разобраться необходимо и в понятии «формализованное доказательство теорем» — это преобразование исходных логических формул (теорем) по 27 правилам логики исчисления предикатов, порядок применения которых однозначно зафиксирован. Формальное или формализованное доказательство позволяет присвоить гипотетическому утверждению статус истинного. Говоря проще, математическая структура — логика предикатов первого порядка позволяет описать мысли человека в виде математических формул и рассматривать вопрос об их истинности уже как утверждение, подлежащее доказательству — в виде теоремы [9]. В теории аксиоматического моделирования предусмотрен формальный метод доказательства теорем, т.е. доказательства истинности без субъективного влияния человека, в высшей математической мере объективный. Надо полагать, что изложенного выше достаточно для понимания математических основ в формировании модели мышления конкретного человека. Таким образом, как нам представляется, логическое произведение концептов знаний, отраженных в статье, использование физической модели мышления [1, 2, 12] и методологии аксиоматического моделирования гарантированно обеспечит построение корректного рефлекторного кольца, «являющегося моделью одной из материализованных элементарных либо составных мыслей этого человека». Само кольцо представляет собой фрагмент нейронной сети человека — постановщика задачи [8, 12]. Целевая теорема для доказательства истинности этого факта будет иметь вид [12]:
(ɄX)((p1(X) Λ p2(X) Λ p3(X) Λ p4(X) Λ p5(X) ˄ p6(X) Λ Λ p7(X)) = > p8(X)) = >
(ƎX)((p1(X) Λ p2(X) Λ p3(X) Λ p4(X) Λ p5(X) Ʌ p6(X) Ʌ Λ p7(X)) = > p8(X)) [1].
Истинность формулы [1], записанной средствами логики предикатов первого порядка, доказывается методом Робинсона для автоматического доказательства теорем и означает корректность предлагаемой модели.
Заключение
Так как в процессе познания мироздания выявляется исключительно логика ее жизнедеятельности, получившая статус естественных законов жизнедеятельности неживой и живой материи, то наиболее подходящей математической структурой для оперирования с логическими функциями является логика предикатов первого порядка. Право фундаментальной основы для всех других наук, связанных с познанием мироздания, логика предикатов первого порядка получила вследствие того обстоятельства, что она регламентирует правила мышления, обеспечивающие корректные причинно-следственные взаимозависимости между силами, вечно и непрерывно движущими материю мироздания.
1. Кондратенко В.А. О математическом моделировании смысла транслируемых текстов // Компьютерная математика. — 2006. — № 1. — С. 27-40.
2. Кондратенко В.А. Создание формальной модели стандартной диалектической логики автоматического управления анатомо-функциональными системами организма человека. 5-я Международная научно-техническая конференция «Информационные системы и технологии» ИСТ-2016 Харьков — Коблево, 12–17 сентября 2016 г. — С. 34-39.
3. Кондратенко В.А. Искусственный интеллект. Замысел и реалии текущего времени на фоне естественного интеллекта человека. — К.: Задруга, 2017. — 84 с.
4. Теленгатор А.Я. Общая теория мышления // Новости медицины и фармации. — 2018. — № 646. — С. 74-76.
5. Теленгатор А.Я. Аттракторы, теория хаоса и вопросы мышления // Мат-ли ХІІІ наук.-практ. конф. «Формування національних і загальнолюдських цінностей у студентів медичних і фармацевтичних вищих навчальних закладів», 21 березня 2013 р. Київ, ФО-П, Сіренко О.В., 2013. — С. 120-122.
6. Теленгатор А.Я. Мышление человека как анализ и синтез информационных составляющих // Мат-ли ХІІІ наук.-практ. конф. «Формування національних і загальнолюдських цінностей у студентів медичних і фармацевтичних вищих навчальних закладів», 21 березня 2013 р. Київ, ФО-П, Сіренко О.В., 2013. — С. 122-124.
7. Теленгатор А.Я. Мышление человека как анализ и синтез физико-химических и культурно-социально-психологических составляющих с точки зрения невролога // Мат-ли ХІІІ наук.-практ. конф. «Формування національних і загальнолюдських цінностей у студентів медичних і фармацевтичних вищих навчальних закладів», 21 березня 2013 р. Київ, ФО-П, Сіренко О.В., 2013. — С. 124-126.
8. Кондратенко В.А. Живая материя в образе формальных моделей (От физиологической наследственности до интеллекта с его активами): Сборник статей автора. — Киев: Юник Принт, 2014. — 186 с.
9. Физиология человека: учебник для мед. вузов / Агаджанян Н.А., Тель Л.З., Циркин В.И., Чеснокова С.А.; под ред. академика РАМН Н.А. Агаджаняна и профессора В.И. Циркина. — М.: Медицинская книга; Н. Новгород: Издательство НГМА, 2003. — 528 с.
10. Анохин П.К. Избранные труды. Кибернетика функциональных систем. — М., 1998. — 395 с.
11. Рубинштейн С.Л. Основы общей психологии. — СПб.: Питер, 2000. — 720 с.
12. Кондратенко В.А. Создание единого стереотипа логической конструкции мышления для содержательного и формального доказательства теорем. — Киев: Алефа, 2010. — 267 с.