Мобильная версия

Журнал «Медицина неотложных состояний» №4(91), 2018

Некоторые вопросы гидродинамики и энергетики циркуляторного и гемического звеньев системы транспорта кислорода (часть 1)

Авторы: Михневич К.Г.
Харьковский национальный медицинский университет, г. Харьков, Украина

Рубрики: Медицина неотложных состояний

Разделы: Справочник специалиста

У 1-й частині статті розглянуто закономірності руху рідини по простій замкненій циркуляторній гідродинамічній системі. Обговорено значення таких показників, як тиск й енергія рідини, що рухається, гідродинамічний опір, вплив на них геометрії гідродинамічного контуру і характеру нагнітальної функції насоса. Наведені моделі порушень кровообігу на прикладі простої замкненої циркуляторної гідродинамічної системи.

В 1-й части статьи рассмотрены закономерности движения жидкости по простой замкнутой циркуляторной гидродинамической системе. Обсуждено значение таких показателей, как давление и энергия движущейся жидкости, гидродинамическое сопротивление, влияние на них геометрии гидродинамического контура и характера нагнетательной функции насоса. Представлены модели нарушений кровообращения на примере простой замкнутой циркуляторной гидродинамической системы.

Part 1 of the article deals with the laws of liquid motion on a simple closed circulatory hydrodynamic system. The value of parameters are discussed such as pressure and energy of a moving fluid, hydrodynamic resistance, the influence on them of the geometry of the hydrodynamic circuit and the nature of the pump discharge function. The models of circulatory disorders are presented on the example of a simple closed circulatory hydrodynamic system.

Ключевые слова

гідродинаміка; гідродинамічний опір; енергія і потужність потоку рідини

гидродинамика; гидродинамическое сопротивление; энергия и мощность потока жидкости

hydrodynamics; hydrodynamic resistance; energy and power of fluid flow

doi: http://dx.doi.org/10.22141/2224-0586.4.91.2018.137851

Поверил

Я алгеброй гармонию.

Сальери (А.С. Пушкин. Маленькие трагедии)

Я располагаю теми же фактами, что и полиция, однако выводы, которые я делаю из этих фактов, моя собственность, которой с полицией я делиться не обязан.

Ниро Вульф, частный детектив, 924, 35‑я Западная улица, Нью-Йорк (Рекс Стаут)

Описательный анатом знает только мертвый материал. Механику недостаточно известен ни живой, ни мертвый организм, чтобы правильно уяснить существующие при этом отношения и структуры. Физиолог будет исследовать функцию живого организма только путем экспериментов. Любое одностороннее исследование, проведенное только с помощью одного метода, недостаточно объективно, чтобы исчерпать гармонические проявления жизни.

П.Ф. Лесгафт

Введение

Живая природа — явление, насколько известно современной науке, уникальное, которое управляется своими уникальными законами. Однако не следует забывать, что живая природа построена из тех же элементов, что и неживая, и что законы неживой природы также действуют и в живой природе. Это относится и к закону сохранения энергии. Определить понятие энергии очень трудно, как и любое фундаментальное понятие. Можно лишь сказать, что для любой природной системы можно определять некую величину, называемую энергией и равную сумме различных составляющих (называемых формами энергии), которая всегда остается постоянной независимо от процессов, происходящих в системе. Энергия может переходить из одной формы в другую (этот процесс называется работой), но общая энергия при этом сохраняет прежнее значение. Этот принцип называют первым началом термодинамики, или законом сохранения энергии [1].

Живому организму, являющемуся частично открытой отграниченной от внешней среды системой [2], энергия необходима прежде всего для поддержания своей целостности в постоянно меняющихся окружающих условиях, которые нередко могут быть весьма неблагоприятными (воздействие различных повреждающих факторов). Живые тела в отличие от неживых стремятся к постоянному снижению энтропии (степени беспорядка), которая в неживых системах неуклонно возрастает (второе начало термодинамики). Снижение энтропии невозможно без притока энергии извне.

Единственный источник энергии на Земле — Солнце (элементы, выделяющие энергию при радио–активном распаде и греющие Землю изнутри, тоже были образованы в недрах Солнца). Солнечная энергия переводится растительными организмами в химическую, которая может быть уже потреблена животными организмами. Химическая сторона энергетических процессов в живых организмах изучается давно, и здесь достигнуты серьезные успехи, хотя проблемы тоже остаются. Одной из них является проблема излишней массы тела у людей. Физиология человека сформировалась в те времена, когда добыча энергии (то есть пищи) сама по себе требовала больших усилий и попытка добычи пищи не всегда оканчивалась успехом. Вследствие этого развились механизмы накопления энергии в собственном теле в виде энергии связи химических соединений, в том числе в виде жиров. Ныне в цивилизованных странах проблема добычи питания решена, большой энергии она не требует, а «стремление к накопительству» осталось. С точки зрения энергетического подхода, обладающего поистине уникальной универсальностью, данная проблема решается просто: на некоторое время нужно придерживаться отрицательного энергетического баланса, то есть затраты энергии должны превосходить ее поступление (проще говоря, нужно меньше есть и больше двигаться). Но здесь уже выступают на сцену законы живой природы, прежде всего психологические.

Итак, добыча энергии сама по себе тоже требует энергии. В критических состояниях потребность в энергии возрастает в 2–4 раза [3], тогда как возможность обеспечить необходимое количество энергии резко снижается. Развивающийся в этих условиях ацидоз снижает скорость потребления кислорода тканями [2]. Энергия живым организмом добывается путем окисления химических ее источников, и, как известно, максимум энергии можно получить при аэробном окислении, то есть, кроме источников энергии, необходимо добывать кислород. У высших животных сформировалась весьма совершенная система транспорта кислорода (СТК) из атмосферы к клетке, и состоит она из 4 звеньев. Дыхательная система доставляет кислород из атмосферы в кровь, где он «садится» в транспортное средство — гемоглобин. Гемоглобин получает кинетическую энергию от системы кровообращения, в первую очередь от миокарда, и направляется к клеткам, которым и передает кислород. Там в митохондриях происходит конечная стадия использования кислорода с выделением энергии и ее запасанием в доступной для организма форме — форме химической связи в молекулах аденозинтрифосфата. Таким образом, нетрудно заметить, что все описанные процессы добывания энергии сами по себе требуют энергии: энергии движения дыхательных мышц и энергии для приведения в движение крови. Это значит, что добыча энергии имеет свою энергетическую цену (или, что практически то же самое, добыча кислорода тоже требует кислорода), равную соотношению между полученной энергией и затратой энергии на ее получение. Эта цена может существенно возрастать при критических состояниях. Таким образом, можно говорить о коэффициенте добычи энергии (КДЭ), как мы говорим о коэффициенте полезного действия (КПД). Но если КПД всегда меньше 1, то КДЭ, наоборот, должен быть всегда больше 1.

Из всех звеньев СТК система кровообращения (СК), пожалуй, играет важнейшую роль. Не случайно развитие сердечно-легочно-мозговой реанимации идет по пути уделения все большего внимания искусственному кровообращению в виде массажа сердца. СК обладает наибольшими компенсаторными возможностями (объемная скорость кровотока может возрастать у здоровых людей в 5 и более раз, чего нельзя сказать о минутном объеме дыхания), но она и потребляет энергии значительно больше, чем другие звенья СТК. В то же время повреждения СК и нарушения в ней зачастую имеют фатальные последствия, поэтому изучение энергетики крово–обращения у критических больных нам представляется чрезвычайно важным.

При изучении СК и лечении ее недостаточности главное внимание уделяют скорости движения крови (а значит, скорости доставки кислорода клеткам), что вполне справедливо. Но в свете вышесказанного не меньшее значение приобретает и энергетический аспект работы СК, поскольку, как мы покажем ниже, одна и та же скорость движения крови может быть достигнута при разных затратах энергии.

О значении энергодефицита в развитии критических состояний догадывались уже давно. Так, например, еще в 1913 году G. Crile рассматривал шок как результат длительного или чрезмерного по интенсивности действия раздражителя на организм, приводящего к исчерпанию энергетических резервов центральной нервной системы, которое протекает в 3 фазы: утомление — истощение — шок [4]. Естественно, с тех пор наши представления о шоке в частности и о критических состояниях вообще претерпели значительные изменения, но за ними энергетический аспект этих состояний почему-то ушел на второй план, хотя само слово «энергия» все чаще мелькает в статьях и монографиях. Мы бы хотели вновь обратиться к энергетическим аспектам жизнедеятельности, упорядочив, по возможности, их понимание. При этом будет полезно временно отвлечься от широко известных истин, о причинах которых уже никто не задумывается.

В данной работе мы уделим главное внимание циркуляторному и гемическому звеньям энерго–снабжения организма. Это потребует подробного рассмотрения некоторых аспектов гидродинамики вообще и в приложении к СК, а также некоторых вопросов, связанных с гемическим звеном СТК.

1. Гидродинамические основы макрогемодинамики

Рассмотрение гидродинамических основ кровообращения мы начнем с простейшей гидродинамической системы, состоящей из замкнутого герметически изолированного от окружающей среды трубопроводного контура с абсолютно жесткими стенками (форма и объем которых не зависят от внешнего и внутреннего давления), внутрь которого включен насос, создающий постоянное по величине и направлению усилие, заставляющее двигаться объем жидкости, заключенный в контур. Затем мы будем эту систему постепенно усложнять, все более приближаясь к реальной СК.

1.1. «Гидродинамический закон Ома» — закон Пуазейля

Вначале рассмотрим течение жидкости по прямолинейному цилиндрическому отрезку трубы с бесконечно жесткими стенками. Этот процесс описывается уравнением Пуазейля:

где Q — объемная скорость течения вязкой несжимаемой жидкости по прямолинейному цилиндрическому отрезку трубы, r — его радиус, l — его длина, η — коэффициент динамической вязкости жидкости, измеряемый в Па∙с, Δp — градиент давлений между началом и концом участка.

Из уравнения (1.1.1) следует, что объемная скорость прямо пропорциональна градиенту давлений (что неудивительно) и некоей величине Эту величину можно назвать коэффициентом проводимости отрезка трубы, однако чаще пользуются обратной величиной и называют ее гидродинамическим сопротивлением:

Таким образом, гидродинамическое сопротивление отрезка трубы прямо пропорционально его длине, динамической вязкости жидкости и обратно пропорционально четвертой (!) степени радиуса трубы.

С учетом уравнения (1.1.2) соотношение (1.1.1) можно представить в виде, называемом модификацией Франка уравнения Пуазейля:

Рассмотрим подробнее каждую из составляющих, определяющих объемную скорость движения жидкости Q.

Градиент давлений Δp требует повышенного внимания. Он создается внешними по отношению к отрезку трубы силами. Если Δp = 0, то движение жидкости отсутствует (конечно, при условии, что в (1.1.3) R > 0). Этот, казалось бы, тривиальный факт часто не осознается, но очень важен и означает, что при движении жидкости по трубе всегда происходит снижение давления, если только R > 0; если же жидкость не движется, то нет и снижения давления, то есть давление по всей длине отрезка трубы одинаково (если пренебречь действием гравитационного поля). Если же R = 0 (идеальный случай), то для поддержания движения жидкости не нужна разница давлений (она нужна только в момент приведения жидкости в движение, если же разницу давлений при нулевом сопротивлении поддерживать постоянной, то скорость движения жидкости по отрезку трубы будет постоянно возрастать). Таким образом, на любом обладающем гидродинамическим сопротивлением отрезке трубы с абсолютно жесткими стенками при движении жидкости происходит снижение давления. Оно тем больше, чем больше гидродинамическое сопротивление трубы и чем больше объемная скорость движения жидкости (что непосредственно следует из (1.1.3)).

При изучении гидродинамики до определенной степени допустимы электротехнические аналогии. Так, уравнение (1.1.3) аналогично закону Ома для участка электрической цепи (справедливости ради следует заметить, что, устанавливая свой знаменитый закон, Г. Ом, как раз наоборот, пользовался гидродинамической аналогией [5], но этот закон настолько знаменит и часто используется, что теперь сам служит моделью для аналогий):

где I — сила тока, U — разность электрических потенциалов, R — электрическое сопротивление.

Гидродинамическое сопротивление при ламинарном течении обусловлено прежде всего трением ближайшего к стенке трубы слоя жидкости, затем — трением следующего слоя о прилежащий к стенке и т.д. Трение ближайшего к стенке слоя жидкости определяется как физико-химическими свойствами стенки, так и свойствами жидкости, трение между слоями жидкости определяется вязкостью жидкости. Если жидкость не обладает вязкостью, несжимаема и трение о стенки трубы отсутствует, то фронт (то есть поверхность, проходящая через точки, находившиеся до начала движения жидкости в одной плоскости, перпендикулярной оси отрезку трубы) движущейся жидкости выглядит как плоскость, перпендикулярная направлению движения жидкости (рис. 1.1.1А).

Если вязкость нулевая, но трение о стенки трубы наблюдается (гипотетический случай), то фронт выглядит, как показано на рис. 1.1.1Б. Если же жидкость вязкая, то фронт движущейся жидкости вытянут вперед и тем больше, чем больше вязкость жидкости (рис. 1.1.1В). Скорость в области центральной оси потока максимальная, у стенок трубы — минимальная.

Выясним, как влияет радиус отрезка трубы на его гидродинамическое сопротивление. Для этого рассмотрим цилиндрический отрезок трубы с заключенной в нем движущейся жидкостью (рис. 1.1.2).

Радиус отрезка трубы равен r, длина отрезка — l, толщина элемента объема жидкости, касающегося стенок трубы, — r_e, причем r = nr_e, где n — некоторое целое положительное число. Будем считать, что r_e количественно отражает вязкость жидкости (чем она больше, тем больше r_e, то есть тем больше элементарных слоев жидкости, или, что то же самое, более толстый слой жидкости тормозится стенками трубы), при этом n отражает радиус трубы.

Объем жидкости в цилиндрическом отрезке V_O:

V_O = pr²l = pn²r_e2l. (1.1.5)

Ясно, что объем элемента жидкости V_eO , испытывающий сопротивление со стороны стенок трубы, равен разнице между всем объемом жидкости V_O и объемом, радиус которого меньше на r_e:

V_eO = p(nr_e)²l – p(n – 1)²r_e2l = pr_e²l(2n – 1). (1.1.6)

Отношение испытывающего трение о стенки объема ко всему объему жидкости равно

Из уравнения (1.1.7) видно, что общий объем жидкости в отрезке цилиндрической трубы V_O пропорционален квадрату радиуса трубы (n²), тогда как объем испытывающей трение жидкости V_eO — первой степени радиуса (n), то есть с ростом радиуса трубы все меньшая часть общего объема жидкости соприкасается со стенками трубы, вследствие чего гидродинамическое сопротивление уменьшается.

1.2. Энергия и мощность потока жидкости

Любое изменение состояния движения возникает лишь под действием силы. При наличии сопротивления движению сила должна действовать постоянно и постоянно совершать работу против сил сопротивления. Если действующая сила по величине равна силе сопротивления и направлена противоположно ей, то состояние движения тела не изменяется, при этом движущая сила непрерывно совершает работу против сил сопротивления. Работа же — это процесс перехода энергии одного вида в энергию другого вида. Если скорость (кинетическая энергия) движущегося тела постоянна, то вся работа движущей силы переходит в тепло.

Все это в полной мере относится и к движению жидкости в трубе. Для поддержания движения жидкости в трубе на жидкость должна действовать сила, распределенная по площади бесконечно тонкого элемента жидкости, равной площади сечения трубы, то есть давление. При рассмотрении замкнутых циркуляторных гидродинамических систем (ЗЦГС), каковой является СК, давление можно представлять как некий потенциал поля действия сил давления. Если в двух областях сосуда эти потенциалы не равны друг другу (имеется разность давлений), кровь движется из области с бóльшим потенциалом в область с меньшим потенциалом.

Рассмотрим короткий участок сосуда (рис. 1.2.1) с площадью поперечного сечения S и длиной Δl. Под действием силы F₁, распределенной по площади S элемента крови, последний перемещается из положения 1 в положение 2, где на него уже действует меньшая сила F₂. Сила уменьшается, поскольку тратится энергия на преодоление сопротивления трубы R, то есть сила совершает работу, которая равна F∙Δl, где F = F₁ – F₂.

Давление же на элемент крови равно

p = F/S. (1.2.1)

S можно представить как

S = V/Δl, (1.2.2)

где V — объем участка сосуда, тогда давление

p = F/S = F/(V/Δl) = FΔl/V. (1.2.3)

Поскольку F∙Δl представляет собой работу (A) по перемещению элемента жидкости, то давление равно

p = F/S = FΔl/V = A/V. (1.2.4)

Этот важный результат означает, что давление, по крайней мере в ЗЦГС, следует рассматривать как работу по перемещению единичного объема жидкости в поле сил давления, и измерять его можно не только в общепринятых единицах, но и в Дж/м³ или эрг/см³ (1 Дж/м³ = 1 Н/м² = 1 Па, 1 эрг/см³ = 1 дин/см²).

Скорость выполнения работы называют мощностью. В нашем случае мощность силы, движущей жидкость, равна

Но то есть объемная скорость тока жидкости, следовательно

P = pQ, (1.2.6)

Учитывая (1.1.3), соотношение (1.2.6) можно представить в виде

Здесь опять уместна электротехническая аналогия. Мощность электрического тока определяется из соотношений:

Электротехническая аналогия помогает по-новому взглянуть и на физический смысл разности давлений. Ведь разность электрических потенциалов является работой по перемещению единичного электрического заряда в электрическом поле. Так же и разница давлений представляет собой работу по перемещению единичного объема жидкости в поле действия сил давления (это следует из (1.2.4)).

1.3. Процесс перемещения объема жидкости по простой замкнутой циркуляторной гидродинамической системе

До сих пор мы говорили об отрезке трубы, теперь перейдем к рассмотрению герметично замкнутого контура трубопровода с бесконечно жесткими стенками (ЗЦГС), внутрь которого помещен насос (например, пропеллер, приводимый в движение расположенным внутри трубы электромотором) (рис. 1.3.1).

Пока насос не работает, во всем контуре отмечается определенное давление жидкости p₀(под давлением в контуре здесь и далее мы будем иметь в виду разницу между давлением в контуре и атмосферным давлением, то есть атмосферное давление принимается за нулевой уровень1), которое определяется затраченной на заполнение контура работой (будем теперь говорить о практически несжимаемой жидкости, такой, например, как вода, то есть о жидкости, объем которой очень слабо, но все же зависит от давления). При соответствующей конструкции лопастей пропеллера вследствие его вращения по одну сторону от него будет создаваться избыток давления (сгущение), а по другую — его снижение (разрежение). Разница давлений будет причиной движения жидкости. Давление со скоростью звука в жидкости начнет передаваться во все участки контура, но, поскольку он обладает гидродинамическим сопротивлением, оно по ходу контура при движении жидкости будет снижаться и достигнет минимума перед насосом (рис. 1.3.2).

Если бы трубопровод не оказывал сопротивления, насос был бы нужен только для сообщения жидкости первоначального импульса, затем его можно было бы выключить, и давление по всему контуру выровнялось бы (в противном случае скорость движения жидкости нарастала бы бесконечно). Чем больше нагнетательная способность насоса, тем больше давление на его выходе по сравнению с p₀и меньше на его входе по сравнению с p₀. Если до и перед насосом перекрыть краны, разница давлений на входе и выходе насоса будет характеризовать его нагнетательную способность, то есть нагнетательная способность насоса — давление, которое он создает при бесконечно большом сопротивлении замкнутого трубопровода (эту характеристику можно назвать движущей, или кинетической, силой насоса по аналогии с электродвижущей силой — источником электрического тока). При открытии кранов разница давлений станет меньше, поскольку насос обладает своим собственным (внутренним) сопротивлением, на котором при движении жидкости также происходит падение давления. Оно тем меньше, чем меньше внутреннее сопротивление насоса, и чем последнее меньше, тем больше резервы мощности у насоса (тем лучше он поддерживает разность давлений при снижении сопротивления контура). Чем меньше сопротивление контура, тем меньше должно быть внутреннее сопротивление насоса для поддержания прежней разницы давлений и прежней скорости движения жидкости. С учетом вышесказанного уравнение (1.1.3) нужно переписать следующим образом:

где F_K — движущая (кинетическая) сила насоса, измеряемая в единицах давления, r — внутреннее гидродинамическое сопротивление насоса, R — гидродинамическое сопротивление контура.

Максимум мощности насос имеет возможность отдать, если сопротивление трубопровода равно внутреннему сопротивлению насоса (КПД насоса при этом равен 50 %): действительно, если сопротивление трубопровода значительно больше сопротивления насоса, скорость движения жидкости очень мала, следовательно, и мощность ее движения мала (КПД максимален), если же сопротивление трубопровода значительно меньше сопротивления насоса («короткое замыкание»), почти все давление будет снижаться на самом насосе, и опять мощность движения жидкости по контуру будет мала (КПД минимален). Максимальной отдаваемая мощность будет при равных внутреннем и внешнем сопротивлениях. В исследовании, посвященном взаимоотношениям между миокардом и сосудами, кстати, отмечено, что в норме жесткость желудочков и артерий одинакова, поскольку при этих условиях энергозатраты на кровообращение минимальны [6], а жесткость стенок сосудов — один из факторов, влияющих на ОПСС.

Это можно проиллюстрировать следующим образом. Общая мощность, затрачиваемая всей системой (насос + трубопровод + циркулирующая жидкость), равна сумме мощностей (см. соотношение (1.2.7)), теряемой в насосе и отдаваемой в контур, которая затрачивается жидкостью на преодоление гидродинамического сопротивления (всю эту мощность насос потребляет от внешнего источника):

P_Σ = P_внутр + Pвнешн = Q2r + Q2R = Q2(r + R),(1.3.2)

где P_Σ – общая мощность, P_внутр — мощность, теряемая при прохождении жидкости через насос, Pвнешн — мощность, отдаваемая в контур.

Тогда с учетом (1.3.1) мощность, отдаваемая в контур, равна

Производная мощности, отдаваемой в контур, по сопротивлению контура имеет вид:

Легко видеть, что экстремум функции (1.3.3) достигается при . При R < r функция нарастает, при R < r — убывает, значит, экстремум является максимумом. На рис. 1.3.3 представлены 2 примера для двух разных внутренних сопротивлений насоса.

1.4. Моделирование нарушений кровообращения на простой замкнутой циркуляторной гидродинамической системе

Если в трубе с бесконечно жесткими стенками открыть кран, позволяющий вытекать жидкости наружу (модель кровотечения или другого первичного снижения ОЦК), то истечение жидкости будет продолжаться до тех пор, пока ее давление в области крана не достигнет атмосферного (рис. 1.4.1А). Малейшее снижение давления жидкости ниже атмосферного (вследствие неустойчивого равновесия давлений жидкости и атмосферы) приведет к тому, что воздух начнет заходить в трубу и вся жидкость из системы вытечет.

Если же к системе подключить дополнительный отрезок трубы с бесконечно жесткими стенками, внутри которого вакуум (модель сосудистой недостаточности, то есть первичного увеличения объема сосудистого русла), то в потоке практически несжимаемой жидкости возникнут пустоты, поскольку свой объем она практически не меняет (рис. 1.4.1Б).

Если снизится производительность (мощность) насоса (модель сердечной слабости), то снизится объемная скорость тока жидкости, давление на выходе насоса будет превышать p₀в меньшей степени, а на входе будет ниже p₀в меньшей степени (рис. 1.4.1В).

1.5. Двухтактный насос

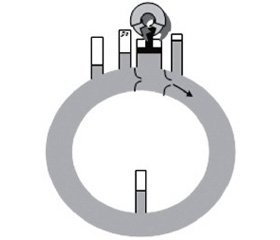
В живой природе (да и в естественной неживой тоже) не встречается вращение тела на валу (недаром изобретение колеса считается одним из величайших достижений человечества), поэтому на первом этапе приближения к СК заменим насос с пропеллером поршневым (двухтактным, то есть с двумя рабочими ходами) насосом и добавим идеальные клапаны с нулевым сопротивлением, позволяющие двигаться жидкости в одном направлении (рис. 1.5.1), продолжая считать стенки контура абсолютно жесткими. Энергию такой насос может получать, например, от руки исследователя.

Пусть работа насоса начинается с движения поршня вниз (модель систолы). Давление в контуре вне клапанов сначала не изменится, давление же между клапанами быстро увеличится, и когда выходной клапан откроется, это увеличение передастся на весь контур со скоростью звука в жидкости, входной клапан откроется. Если на этом работа насоса прекратится, давление в контуре выровняется на более высоком по сравнению с исходным уровнем p₀ (объем контура за счет хода поршня вниз уменьшился, соответственно этому выросло давление жидкости). Если жидкость малосжимаема, то и ход поршня вниз будет небольшим. Работа, совершенная поршнем насоса за время его движения вниз, равна

A = pΔV, (1.5.1)

где p — среднее давление под поршнем, ΔV — изменение объема под ним (его можно назвать ударным объемом).

Движение поршня вверх, так же как и при движении вниз, требует энергии (ход вверх тоже рабочий)2. При движении поршня вверх (модель диастолы) давление в контуре после выходного клапана сначала не меняется, так как он закрывается, перед поршнем — снижается, жидкость поступает в насос. Если давление жидкости перед насосом станет ниже атмосферного, то для дальнейшего движения поршня вверх потребуется дополнительная энергия для преодоления атмосферного давления (чрезмерное расширение полости насоса может привести к возникновению в потоке практически несжимаемой жидкости пустот и переходу течения в турбулентное, на что потребуется дополнительный расход энергии). Благодаря абсолютной жесткости стенок контура снижение давления быстро передастся на весь контур, и оно вновь выровняется, став теперь ниже исходного p₀. При движении поршня вверх насос выполнит работу, данную в соотношении (1.5.1).

Таким образом, в рассмотренной системе невозможно достичь большого хода поршня (ударного объема), так как жидкость практически несжимаема, а стенки контура абсолютно жесткие. Поток жидкости всегда будет пульсирующим, его скорость будет колебаться между ≈ 0 и какой-то положительной величиной, а для обеспечения непрерывности потока (время, в течение которого скорость минимальна, стремится к 0) частота работы насоса должна быть увеличена. Увеличение объемной скорости жидкости возможно только за счет роста частоты, так как в рассмотренных условиях увеличение ударного объема практически неосуществимо.

При напряженном заполнении контура (первоначальное давление p₀ высокое — модель гиперволемии или сосудистого спазма), когда «преднагрузка» насоса велика, расход энергии на расширение полости насоса будет небольшим (дополнительно используется энергия, затраченная на напряженное заполнение контура), зато «постнагрузка» при этом большая, поэтому расход энергии на сокращение полости насоса будет большим. В обратном случае (модель гиповолемии или сосудистой слабости) больше энергии будет расходоваться на расширение полости насоса. Важно отметить, что энергия, которая потребляется насосом от внешнего источника (скажем, руки исследователя), требуется как при движении поршня вниз («систола»), так и при движении вверх («диастола»).

Конфликт интересов. Автор заявляет об отсутствии какого-либо конфликта интересов при подготовке данной статьи.

Список литературы

1. Купер Л. Физика для всех. Т. 1: пер. с англ. С.Н. Бреуса / Л. Купер; под ред. Ю.А. Кравцова. — М.: Мир, 1973. — 479 с.

2. Усенко Л.В. Интенсивная терапия при кровопотере / Л.В. Усенко, Г.А. Шифрин. — 3-е изд., концептуальное и инновационное. — Днепропетровск: Новая идеология, 2007. — 290 с.

3. Рябов Г.А. Гипоксия критических состояний / Г.А. Рябов. — М.: Медицина, 1988. — 288 с.

4. Шок: теория, клиника, организация противошоковой помощи / Под общ. ред. Г.С. Мазуркевича и С.Ф. Багненко. — СПб.: Политехника, 2004. — 544 с.

5. Роджерс Э. Физика для любознательных. Т. 3. Электричество и магнетизм. Атомы и ядра: пер. с восьмого амер. изд. / Э. Роджерс; под. ред. В.Ф. Киселева, общ. ред. Л.А. Арцимовича. — 2-е изд., испр. — М.: Мир, 1973. — 664 с.

6. Chirinos J.A. Ventricular-arterial coupling: invasive and non-invasive assessment // Arthritis Res. — 2013. — 7(1). — Р. 2-14.