Мобильная версия

Журнал «Медицина неотложных состояний» №5(92), 2018

Некоторые вопросы гидродинамики и энергетики циркуляторного и гемического звеньев системы транспорта кислорода (часть 2)

Авторы: Михневич К.Г.
Харьковский национальный медицинский университет, г. Харьков, Украина

Рубрики: Медицина неотложных состояний

Разделы: Справочник специалиста

У 2-й частині статті подано закономірності руху крові по системі кровообігу як замкненій циркуляторній гідродинамічній системі (ЗЦГС). Показано значення елементів ЗЦГС, що здатні змінювати свою форму і об’єм під впливом змін тиску та об’єму циркулюючої рідини та відповідають різним відділам судинної системи. Розглянуто питання про вибір одиниць вимірювання для оцінки стану системи кровообігу. Велику увагу приділено принципам нормування гемодинамічних показників.

Во 2-й части статьи представлены закономерности движения крови по системе кровообращения как замкнутой циркуляторной гидродинамической системе (ЗЦГС). Показано значение элементов ЗЦГС, способных изменять свою форму и объем под влиянием изменений давления и объема циркулирующей жидкости и соответствующих разным отделам сосудистой системы. Рассмотрен вопрос о выборе единиц измерения для оценки состояния системы кровообращения. Большое внимание уделено принципам нормировки гемодинамических показателей.

The 2nd part of the article presents the laws of blood flow through the circulatory system as a closed hydrodynamic circulatory system (CCHS). The value of the CCHS elements that can change its form and volume under the influence of changes in pressure and circulating fluid volume and corresponding to different parts of the vascular system has been shown. The choice of units of measurement for assessing the state of the circulatory system is considered. Much attention is paid to the principles of normalization of hemodynamic parameters.

Ключевые слова

гідродинаміка; гідродинамічний опір; енергія та потужність потоку рідини; недостатність кровообігу

гидродинамика; гидродинамическое сопротивление; энергия и мощность потока жидкости; недостаточность кровообращения

hydrodynamics; hydrodynamic resistance; energy and power of fluid flow; circulatory failure

doi: http://dx.doi.org/10.22141/2224-0586.5.92.2018.143228

1.6. Приближение простой замкнутой циркуляторной системы к реальной системе кровообращения: реактивные элементы

Стенки реального контура обязательно обладают некоторой растяжимостью, хотя, возможно, и исчезающе малой. На следующем этапе приближения к системе кровообращения (СК) для удобства весь контур можно разделить на элементы, имеющие только резистивное (активное) гидродинамическое сопротивление с абсолютной жесткостью стенок, и элементы с реактивным сопротивлением, податливыми стенками и нулевым резистивным сопротивлением. Реактивные элементы могут менять форму и объем в зависимости от давления в них (рис. 1.6.1). Пусть при этом после насоса по ходу тока жидкости сначала располагается элемент небольшого диаметра с абсолютно жесткими стенками (назовем его резистивным элементом высокого давления (РЭВД)), затем — элемент того же диаметра с эластичными стенками, которые могут немного растягиваться при повышении давления в них (индуктивный элемент высокого давления (ИЭВД)), далее — ряд параллельно соединенных элементов малого диаметра (резистивные элементы пониженного давления (РЭПД)), с каждым из которых параллельно соединен реактивный емкостный элемент пониженного давления (ЕЭПД), затем — элемент большого диаметра с абсолютно жесткими стенками (резистивный элемент низкого давления (РЭНД)), параллельно с которым соединен элемент наибольшего диаметра с очень податливыми стенками (емкостный элемент низкого давления (ЕЭНД)).

Добавление реактивных элементов значительно изменит картину движения жидкости в контуре. В отсутствие движения жидкости давление в контуре будет по-прежнему везде одинаково, но на форму контура теперь будет оказываться не только давление жидкости, но и внешнее, атмосферное, давление. Если контур заполнен жидкостью достаточно напряженно (то есть давление в нем превышает атмосферное), то сечение всех элементов контура будет иметь форму, близкую к окружности.

Вновь начнем работу насоса с движения поршня вниз. Благодаря входному клапану (перед насосом) повышение давления будет передаваться только в одном направлении — в сторону РЭВД. Давление в РЭВД будет нарастать медленнее, чем в отсутствие ИЭВД, поскольку объем последнего будет несколько увеличиваться вследствие эластичности его стенок. Часть энергии насоса будет накапливаться в виде потенциальной энергии растянутых стенок ИЭВД, часть уйдет на преодоление сопротивления РЭВД и часть — на сообщение жидкости кинетической энергии. Когда поршень достигнет наинизшей точки, движение жидкости не прекратится, так как запасенная в стенках ИЭВД энергия начнет переходить в кинетическую энергию жидкости (проще говоря, эластичный элемент начнет сжиматься, возвращаясь в исходное состояние и не давая давлению резко упасть), а клапаны позволят жидкости двигаться только в одном направлении. Постепенно рост давления будет передаваться к последующим элементам, но благодаря их гидродинамическому сопротивлению этот рост будет затухать, и в последнем — емкостном — элементе давление будет повышаться медленнее всего, поскольку кроме предшествующих резистивных элементов этому будет способствовать податливость стенок емкостного элемента, вследствие чего его объем легко увеличивается. Когда вся энергия двигавшегося вниз поршня будет израсходована, жидкость остановится, давление во всем контуре опять выровняется, и его величина будет зависеть от степени уменьшения объема всего контура. Если стенки емкостного элемента настолько податливы, что его объем увеличится ровно настолько, насколько уменьшился объем под поршнем, величина давления вернется к исходной — p₀.

Добавление реактивных элементов облегчит движение поршня вверх, поскольку снижению объема элементов, из которых засасывается жидкость, через их податливые стенки будет способствовать атмосферное давление (поршню будет легче, чем до включения реактивных элементов, преодолевать атмосферное давление, но все же некоторая энергия потребуется на преодоление небольшого сопротивления РЭНД). Чем выше исходное давление p₀ в контуре (чем более напряженно заполнен контур, что соответствует большему ОЦК — в абсолютно жестком контуре объем циркулирующей жидкости увеличить практически невозможно), то есть чем выше преднагрузка, тем легче поршню двигаться вверх, тем больший объем он может засосать. Чем больший объем жидкости входит в насос, тем больше снижается давление в емкостном элементе низкого давления и его объем. Благодаря закрытому выходному клапану насоса снижение давления элементам высокого давления будет передаваться только в направлении против тока жидкости и очень медленно из-за наличия резистивных и емкостных элементов пониженного давления. После того как поршень достигнет наивысшей точки, движение жидкости постепенно прекратится, давление в контуре вновь выровняется и вернется к исходному p₀.

Следующий шаг к приближению рассматриваемого контура к реальной СК состоит в увеличении частоты работы поршня до такой степени, чтобы движение жидкости не успевало полностью останавливаться. Тогда поток жидкости будет пульсирующим и непрерывным, а давление в разных участках контура будет изменяться по-разному, при этом, согласно принципу Бернулли, в любых участках контура величина

(ρ — плотность жидкости, v — линейная скорость движения жидкости) будет постоянной [1].

В элементах высокого давления во время хода поршня вверх давление, как уже было показано, будет снижаться медленнее, чем в самом насосе, и когда оно понизится до определенной ненулевой величины (то есть останется выше атмосферного), поршень вновь начнет двигаться вниз, давление в элементах высокого давления вновь начнет повышаться до максимального уровня, равного максимальному давлению под поршнем. Таким образом, давление под поршнем будет колебаться от практически нулевого до некоторой максимальной величины, определяемой нагнетательной способностью насоса, в элементах же высокого давления колебания окажутся сглаженными, минимальное давление будет выше 0, максимальное — примерно равным максимальному давлению в насосе. Далее, по ходу контура, давление благодаря резистивным элементам будет снижаться, как и его пульсации, и в емкостных элементах оно будет минимальным, а пульсации — практически нулевыми. Чем большую энергию в единицу времени насос будет передавать циркулирующей жидкости, тем выше будет давление в элементах высокого давления (артериальное давление (АД) в СК) и ниже в элементах низкого давления (центральное венозное давление (ЦВД) в СК) и тем больше будет объемная скорость движения жидкости (сердечный выброс (СВ) в СК). Если нагнетательная способность насоса снизится, то уменьшится и разница давлений между элементами высокого и низкого давления (в СК — снижение АД и повышение ЦВД), причем и в том, и в другом элементе это давление будет приближаться к p₀ с той лишь разницей, что в элементах низкого давления оно будет расти, а в элементах высокого давления — снижаться.

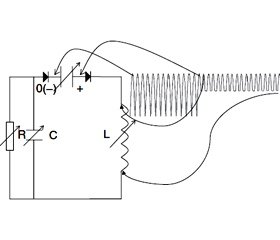
Прибегая опять к электротехнической аналогии, участки контура с абсолютно жесткими стенками можно уподобить активному электрическому (резистивному) сопротивлению, емкостные элементы – электрической емкости, а индуктивные — электрической индуктивности. Для полноты аналогии добавим, что клапаны — аналоги электрических диодов (рис. 1.6.2). Энергия теряется только в активном сопротивлении, в реактивном же она периодически запасается и расходуется. Поскольку направление тока жидкости постоянно, емкости в электротехнической аналогии включены параллельно резистивным и индуктивным элементам (конденсаторы не пропускают постоянную составляющую тока).

1.7. Модели нарушений кровообращения при наличии реактивных элементов

Повторим теперь все описанные выше мысленные эксперименты при наличии реактивных элементов. Если в системе открыть кран (модель первичного снижения ОЦК), или снизить нагнетательную способность насоса (модель сердечной слабости), или подключить параллельно контуру дополнительные трубки (модель первичного увеличения объема сосудов — сосудистой недостаточности), то в некотором участке контура со свойствами реактивного элемента объем и давление жидкости начнут снижаться, и благодаря податливости стенок участка контура его объем под действием атмосферного давления тоже снизится в соответствии со снижением объема жидкости, объемы жидкости и участка контура останутся равными. Если при этом считать длину сечения сосуда неизменной, то оно из круглого перейдет в эллипсоидное. Переход к эллипсоидной форме сечения участка контура (в пределе — почти плоской) приведет к тому, что объем циркулирующей жидкости начнет соприкасаться с внутренней поверхностью сосудов большей площади (рис. 1.7.1). Но поскольку одной из составляющих гидродинамического сопротивления является трение жидкости о внутреннюю поверхность контура, следовательно, при наличии тока жидкости гидродинамическое сопротивление возрастет и снижение давления увеличится.

При спадении участка контура и неизменной длине окружности его сечения (2πr) спавшийся участок можно рассматривать с определенной степенью приближения как параллелепипед со сторонами l, d и (2πr – 2d) / 2 = πr – d (при этом 0 < d < ½πr, по-прежнему r = nre). d отражает степень спадения сосуда. Объем участка контура составит

Если продифференцировать V_◊ по d, то получим

из чего следует, что максимальный объем достигается при d = ½πr, то есть когда сечение сосуда квадратное, а в пределе — круглое (что при спадении сосудов не наблюдается). В этом случае V_◊ = ¼π2r2l, что в 4/π ≈ 1,3 раза меньше (V_○ / V_◊ = πr2l / ¼π2r2l = 4/π ≈ 1,3), чем если сечение сосуда будет круглым с той же длиной сечения. Чем меньше d, то есть чем больше спался участок, тем меньше его объем.

Объем жидкости, испытывающий трение о спавшиеся стенки участка, равен

и не зависит от степени спадения участка. Отношение испытывающего трения объема ко всему объему жидкости в спавшемся сосуде равно

из чего видно, что при увеличении степени спадения участка (уменьшении d) все большая часть объема жидкости соприкасается со стенками участка (объем жидкости больше «размазывается» по стенке участка).

Зависимость объема спавшегося участка сосуда от степени его спадения показана на рис. 1.7.2.

Повторим наши рассуждения применительно к условию (трудно осуществимому в неживой системе), при котором периметр сечения какого-либо отрезка контура может уменьшаться, сохраняя форму сечения круглой (то есть в условиях уменьшения радиуса круглого сечения контура). При снижении объема жидкости, поступающей в этот отрезок контура, соответственно снизится и объем контура, но если его сечение останется круглым (например, вследствие α-адренергической импульсации, если еще больше приблизиться к сосудистой системе), а его радиус r уменьшается в m раз, то мы получим следующую картину. Площадь соприкосновения объема крови со стенками участка контура будет равна

S_○ = 2π(r/m)l, (1.7.5)

а объем участка контура будет равен

V_○ = π(r/m)²l, (1.7.6)

то есть площадь стенок участка уменьшилась в m раз, а объем участка — в m2 раз, что означает увеличение относительной площади соприкосновения объема крови со стенками сосуда в m раз.

Если теперь потребовать, чтобы объем участка сосуда изменялся в равной степени при переходе его сечения в форму, близкую к прямоугольной, и при уменьшении его диаметра при сохранении круглой формы, то есть чтобы V_○ = V_◊ и, следовательно, dl(πr – d) = π(r/m)²l, то, решая это уравнение относительно d, получим

где m показывает, во сколько раз уменьшился радиус круглого сосуда, d — длину одной из сторон прямоугольного сечения спавшегося сосуда того же объема. Смысл знака «±» заключается в том, что у прямоугольника имеется по 2 стороны равной длины и сумма их длин постоянна. Решение уравнения возможно при m ≥ 1,12837916709552, при меньших значениях m переход в прямоугольную форму невозможен (подкоренное выражение становится отрицательным). Графически зависимость 1.7.7 показана на рис. 1.7.3, из которого видно, что чем больше сократится круглый сосуд (чем больше m), тем более плоским должен стать сосуд при неизменных длине его сечения и объеме, что неизбежно ведет к росту гидродинамического сопротивления. Это подтверждает чрезвычайно важную роль вазоконстрикции, сохраняющей круглую форму сечения сосуда при снижении поступающего объема крови в участок сосудистого русла.

Пусть имеется некоторый отрезок контура, который может изменить свой объем двумя способами: 1) уменьшив свой радиус; 2) не изменив длины своего сечения, стать более плоским, так что форма его сечения из круглой перейдет в близкую к прямоугольной. В обоих случаях объем уменьшится в равной степени (V_○ = V_◊).

В первом случае отношение объема жидкости к площади его соприкосновения со стенками отрезка равно

а во втором —

то есть во втором случае тот же объем приходится на площадь, в m раз большую, что ведет к росту гидродинамического сопротивления.

Таким образом, если в герметично замкнутом контуре неживой системы с резистивными и реактивными элементами снижается объемная скорость жидкости вследствие снижения нагнетательной способности насоса, или изъятия части объема жидкости из контура, или увеличения объема контура путем подключения к нему пустых элементов, заполняемых неизменным объемом жидкости контура, то, поскольку объемы жидкости и контура в силу практической несжимаемости жидкости и податливости стенок контура остаются равными, реактивные участки контура меняют свою форму с круглой на плоскую (приближенно — прямоугольную). При этом большая часть объема жидкости начинает соприкасаться со стенками контура, что ведет к росту гидродинамического сопротивления. Поддержание объемной скорости может быть достигнуто благодаря увеличению частоты работы насоса (в СК — тахикардия), увеличению его нагнетательной способности (в СК — например, использование β₁-адреномиметиков), добавлению некоторого объема жидкости в контур (инфузия) или уменьшению длины сечения контура с сохранением его круглой формы (вазопрессоры). Последнее в неживых системах практически неосуществимо, поэтому остается сделать последний шаг в приближении к реальной СК.

В действительности не бывает элементов с чисто активным или реактивным (емкостным и индуктивным) сопротивлением, все они обладают в той или иной мере всеми видами сопротивления, или гидродинамическим импедансом. Так же и в СК по всем ее участкам «размазаны», хотя и неравномерно, все виды гидродинамического сопротивления (например, аорта и крупные артерии в основном обладают индуктивным сопротивлением, полые вены — в основном емкостным, включенным параллельно низкому резистивному и индуктивному; далее этот вопрос мы рассмотрим подробнее). Важно обратить внимание на следующий факт: объем циркулирующей жидкости (крови) всегда равен объему контура, поскольку он герметичен и замкнут, а выражение «объем сосудов должен соответствовать объему циркулирующей крови» надо понимать в том смысле, что оптимальные условия для циркуляции крови создаются в том случае, когда сечение сосудов сохраняет форму, близкую к окружности.

2. Единицы измерения

Перед тем как переходить к рассмотрению реальной гемодинамики, нам представляется чрезвычайно важным определиться в системе единиц измерения, наиболее подходящей для биологических и медицинских исследований вообще и для изучения циркуляторного и гемического звеньев СТК в частности. Этот вопрос нами ранее уже обсуждался [2], поэтому скажем лишь, что мы остановили свой выбор на системе СГС («сантиметр — грамм — секунда») как наиболее соответствующей из существующих размерам решаемых задач. В ряде случаев конечные результаты имеет смысл приводить в единицах СИ как более привычных.

Более подходящей для медицины, на наш взгляд, была бы система «дециметр — килограмм — минута» (ДКМ), поскольку характерные объемы измеряются в литрах (кубических дециметрах), масса 1 литра воды равна 1 кг, а характерное время в медицине измеряют минутами. Мы попытались создать систему, основанную на этих единицах, однако эта система оказалась настолько непривычной, что вряд ли она найдет сейчас достаточное понимание и распространение. Трудности возникли сразу же при попытке ввести единицу давления для этой системы. Ведь давление имеет размерность силы, деленной на площадь, а сила — массы, умноженной на длину и деленной на квадрат времени (MLT^‑2), то есть размерность давления ML^‑1T^‑2. Чтобы приспособить единицу давления к системе «килограмм — дециметр — минута», пришлось вводить новую единицу силы (хотя сила непосредственно редко измеряется в биомедицинских исследованиях) да еще дать ей название (например, «форт»). Также потребовались новые единицы для измерения ОПСС, работы, мощности и т.д. По этим причинам мы пока отказались от предложения этой системы и приводим ее без комментариев в приложении.

3. Макрогемодинамика

Система кровообращения является одним из звеньев системы транспорта кислорода (СТК), и главной ее функцией является доставка кислорода из легких к клеткам, где он используется для получения энергии. Скорость доставки кислорода определяется, в частности, объемной скоростью кровотока, то есть СВ, при этом он должен быть таким, чтобы потребности тканей в кислороде удовлетворялись.

СК состоит из 3 составных частей: миокардиальный насос, сосудистая система и объем циркулирующей крови (ОЦК), в ней заключенный. Сосудистая система представляет собой типичную ЗЦГС — замкнутый герметичный круг разветвляющихся и соединяющихся вновь сосудов и состоит из двух последовательно соединенных отделов: малая петля, или легочное кровообращение (между правым желудочком (ПЖ) и левым предсердием (ЛП) — то, что принято называть малым кругом), и большая петля, или системное кровообращение (между левым желудочком (ЛЖ) и правым предсердием (ПП) — то, что принято называть большим кругом). Мы предпочитаем не называть отделы сосудистой системы кругами, поскольку они таковыми на самом деле не являются и такое название иногда приводит к недоразумениям.

Кровь, находясь в герметически замкнутом объеме сосудов и миокарда, даже в покое испытывает определенное давление со стороны сосудистых стенок. Это давление определяется объемом крови (всегда равным объему сосудов), гравитационным воздействием и жесткостью сосудистых стенок. При определенном объеме крови и определенной жесткости сосудистых стенок давление покоящейся крови может быть равным атмосферному. При повышении объема покоящейся крови (более напряженное заполнение сосудистой системы) давление крови может превышать атмосферное. Ниже атмосферного это давление может быть (в отсутствие кровотока и дыхания) только в случае очень большой (практически бесконечно большой) жесткости сосудистых стенок и малого объема крови, чего практически не бывает. При наличии кровотока в тех отделах сосудов, которые не могут спадаться в силу анатомических особенностей (жесткая связь с окружающими жесткими тканями, как, например, у v. subclavia), давление может быть в ряде случаев и меньше атмосферного. При определении кровяного давления мы атмосферное давление принимаем за нулевое, и, таким образом, если АД равно 120/80 мм рт.ст., это означает, что на эту величину давление крови выше, чем атмосферное. Если давление ниже атмосферного (например, ЦВД), мы его представляем как отрицательное.

3.1. Отделы сосудистой системы

С точки зрения макрогемодинамики сосудистая система (СС) из всех составных частей СК представляется наиболее сложно устроенной (миокард мы будем рассматривать пока просто как насосный орган, внутри которого заключен оксигенатор со своей сосудистой системой — легкие). СС состоит из нескольких отделов, у каждого из которых есть два названия: анатомическое и физиологическое (рис. 3.1.1).

Из левой половины сердца (ЛС) исходят сосуды высокого давления (СВД; в зарубежной литературе их еще называют сосудами котла; модель этих сосудов — РЭВД и ИЭВД, см. подраздел 1.6). Роль этих сосудов играют аорта и крупные артерии (А). Эти сосуды выполняют две функции, одна из которых пассивна, другая — активна.

Пассивная функция заключается в распределении кровотока по всем зонам организма, то есть СВД являются своего рода трубопроводами. Активная функция СВД связана со свойствами их стенок, а именно — с их эластичностью. Во время систолы они растягиваются, запасая часть энергии сокращения миокарда, во время диастолы (когда аортальный клапан закрыт) запасенная энергия отдается кровотоку, что поддерживает в этот период движение крови по сосудам и снижает скорость снижения давления в них (в ЛЖ в это время давление очень быстро снижается почти до 0). К моменту следующей систолы давление в СВД успевает снизиться до определенной ненулевой величины, называемой диастолическим АД (АДд, p_Dsc). Таким образом, СВД — это ИЭВД, их активная функция заключается в создании АДд, то есть в сглаживании пульсаций АД. При абсолютно жестких стенках сосудов давление в них в диастолу очень быстро снижалось бы практически до 0. Известно, что при выраженном уплотнении стенок артерий (атеросклероз, артериосклероз) АДд ниже нормы.

Динамика кровяного давления во всей СС представлена на рис. 3.1.2.

За сосудами высокого давления следуют артериальные резистивные сосуды (АРС; модели этих сосудов — РЭПД и ЕЭПД, причем первые играют более выраженную роль, чем вторые), или артериальные сосуды сопротивления. Роль этих сосудов играют артериолы. Эти сосуды благодаря α₁-адренергическим механизмам способны менять свои размеры и жесткость, сохраняя круглую форму сечения и влияя, таким образом, на ОПСС. Следующий отдел — сосуды обмена (капилляры), в начале и конце которых находятся сфинктеры, регулирующие кровоток в капиллярах (модель этих сосудов — тоже РЭПД, сфинктеры, и ЕЭПД, сами капилляры, не имеющие в своих стенках мышечных элементов). Регуляция осуществляется прежде всего под влиянием местных условий в окружающей ткани (при сдвиге pH в кислую сторону сфинктеры раскрываются, в основную — прикрываются). Далее кровь направляется в венозные резистивные сосуды (ВРС, их модель — ЕЭНД и РЭНД, причем первые играют более выраженную роль, чем вторые), или венозные сосуды сопротивления. Эти сосуды в основном влия–ют на объем сосудистого русла посредством тех же механизмов, регулирующих тонус АРС. Последний отдел — емкостные сосуды, ЕС (крупные вены; их модель — ЕЭНД), названные так потому, что основная часть ОЦК (до 80 %) размещается именно там.

Таким образом, легко увидеть, что СК представляет собой ЗГЦС с одним кругом кровообращения (рис. 3.1.1).

3.2. Гемодинамические показатели

Перепишем теперь соотношение 1.1.3 применительно к СВ:

где p_sc — общее перфузионное давление системного кровообращения (ОПДСК), равное разнице между средним АД (в дальнейшем — эффективным АД, АД_Э, p_AEF) и ЦВД (p_CVP), R_sc — ОПСС системного кровообращения, p_pc — общее перфузионное давление легочного кровообращения (ОПДЛК), R_pc — ОПСС легочного кровообращения. Ясно, что СВ системного и легочного кровообращения одинаковы.

Расчет значения АД_Э требует пояснения. Давление в СВД носит выраженный пульсирующий характер, поэтому для его оценки необходимо пользоваться так называемым эффективным значением. Эффективное давление — это такое давление, которое, будучи постоянным по величине, выполнит при том же ОПСС ту же работу, что и реальное переменное давление за то же время. Реальное АД можно представить как сумму двух давлений, одно из которых постоянное (диастолическое АД — АД_Д, p_Dsc), а второе — переменное, меняющееся от АД_Д до АДС (систолического АД, p_Ssc). Известно, что квадрат эффективного значения любой величины, в том числе переменной, численно равен площади под кривой, изображающей на графике эту величину, что для эффективного значения переменной части АД (p_ef) математически можно выразить соотношением

где p — мгновенное значение переменной составляющей АД, T — период колебаний давления, то есть величина, обратная ЧСС, t — время, в течение которого давление выполняет работу.

Форму колебаний АД можно приближенно считать синусоидальной, тогда после интегрирования получаем

где p_max — амплитуда переменной составляющей АД, равная половине пульсового давления. Тогда АД_Э можно представить как сумму АД_Д (постоянная величина) и эффективного значения переменной части:

то есть как сумму диастолического и трети пульсового давления.

Вернемся к обсуждению членов равенства 3.2.1. ОПДСК (p_sc) — разница давлений между аортой и внутригрудными венами, являющаяся причиной движения крови и отражающая работу по перемещению единичного объема крови от ЛЖ к ПП.

ОПСС определяется соотношением 1.1.2, однако в клинической физиологии кровообращения это соотношение не может иметь практической ценности по многим причинам. Прежде всего сосудистая система чрезвычайно далека от идеальной гладкой прямолинейной трубы с известными диаметром и длиной. Кроме того, измерение вязкости крови представляет собой сложную задачу, поскольку в разных отделах сосудистого русла она неодинакова. В связи с этим нам кажется, что ОПСС (точнее, обратная ему величина 1/R) должно рассматриваться только как коэффициент пропорциональности в 3.2.1, отражающий некоторые свойства сосудистой системы (в частности, тонус, диаметр сосудов и общую эквивалентную длину сосудистого русла) и самой крови (в частности, вязкость и плотность). Из этого нетрудно сделать вывод, что на ОПСС нельзя так же просто влиять, как на сократительную способность миокарда (например, с помощью β₁-адреномиметиков) или на объем циркулирующей крови (с помощью инфузионной терапии), поскольку оно зависит от очень многих факторов и сосудистый тонус — лишь один из них. Можно сказать, что это является проявлением биологического принципа неопределенности, сходного с принципом неопределенности Гейзенберга в физике [3].

Мощность кровотока (МК) системного (P_sc) и легочного (P_pc) кровообращения равна

С учетом КПД сердца (≈ 30 %) затрачиваемая мио–кардом на кровоток мощность (ММ) будет в соответствующее количество раз больше.

Из 3.2.1 ясно, что один и тот же СВ может иметь место при разных АД и ОПСС, причем если ОПДСК и ОПСС повышаются в n раз, то СВ не меняется, а МК возрастает тоже в n раз, то есть энергозатраты на один и тот же СВ могут быть разными. Поэтому логично ввести показатель, характеризующий удельную МК, равную отношению МК к СВ (P_sc/Q), и этим показателем оказывается p_sc, то есть ОПДСК. К этому выводу мы уже пришли ранее, выяснив, что давление крови представляет собой работу по перемещению единичного объема крови от ЛЖ к ПП.

3.3. Процесс перемещения объема крови по сосудистой системе

Повторим рассуждения, касающиеся движения жидкости по ЗЦГС с реактивными элементами, применительно к реальной СК. Начнем опять с гипотетического момента, когда кровь в СК покоится. В зависимости от напряженности заполнения кровью сосудистой системы (что определяется ОЦК и свойствами стенок сосудов) в ней имеется большее или меньшее давление крови (p₀).

В момент начала систолы желудочков (модель — движение поршня двухтактного насоса вниз) кровь приходит в движение. Желудочки уменьшаются в объеме, давление в них становится выше давления в сосудах, и кровь выбрасывается из сердца через аортальный и легочный клапаны в сосудистую систему. Благодаря растяжимости сосудистых стенок СВД объем крови вовлекается в движение постепенно, так как часть выброшенного объема занимает увеличивающийся объем СВД. Давление в СВД постепенно становится выше исходного (p₀). Затем наступает активное увеличение объема полостей сердца (диастола), а выходные клапаны сердца (аортальный и легочной артерии) закрываются. То, что диастола — активный процесс, подтверждается многими фактами, в частности и гемодинамическими. Во время диастолы желудочков происходит систола предсердий, которые, как известно, не имеют входных клапанов (во всяком случае, ЛП). Тем не менее кровь из предсердий перемещается в желудочки, а не ретроградно, а для этого желудочки должны растянуться так, чтобы давление в них стало меньше давления в полой вене и легочной артерии, для чего требуется дополнительная энергия.

Во время диастолы давление в СВД снижается постепенно благодаря «поджимающему» воздействию их стенок при возвращении в исходное нерастянутое состояние. Давление же в желудочках снижается значительно быстрее, лишь слегка превышая атмосферное на пике диастолы (порядка 2 мм рт.ст.), благодаря чему кровь засасывается из емкостных сосудов, в которых вследствие этого давление становится ниже исходного (p₀). Когда давление в СВД снижается до некоторой величины (70–80 мм рт.ст.), начинается новая систола и все повторяется, постепенно весь объем крови приходит в движение.

Поскольку кровоток по СК и объем сосудистого русла являются пульсирующими, СК можно рассматривать как своеобразный колебательный контур, в котором источник энергии (миокард) возбуждает колебания давления и объемной скорости кровотока. К сожалению, определить резонансную частоту такого контура технически чрезвычайно трудно, если вообще возможно, но вполне возможно, что в состоянии покоя ЧСС как раз и совпадает с резонансной частой СК. Во всяком случае, это может быть одним из перспективных направлений исследования физиологии СК.

3.4. Нормировка гемодинамических показателей

Медицинские и биологические науки имеют дело со многими однородными объектами, различающимися по многочисленным параметрам, такими, например, как масса, линейные, квадратичные и кубичные размеры (рост, площадь поверхности, объем тела человека), поэтому естественным выглядит стремление ввести нормированные показатели изучаемых величин, на которые вышеупомянутые параметры не влияют, что позволит проводить сравнение разных объектов по какому-то параметру. Примерами нормированных показателей могут служить дозы лекарственных препаратов, измеряемых в мг/кг или даже в

мг/кг∙мин, или объем инфузии, выраженный в

мл/кг. Разумным кажется и введение нормированного СВ. Общепринятым является отнесение СВ к площади поверхности тела (ППТ), однако нам кажется, что такая привычная уже величина, как сердечный индекс (СИ — отношение СВ к ППТ), требует по крайней мере обсуждения. Попутно заметим, что все показатели систем транспорта кислорода в интенсивной терапии рассматриваются в состоянии покоя, то есть когда имеет место лишь основной обмен.

Логично предположить, что чем больше тело человека, тем больший СВ требуется для обеспечения тканей кислородом. Но целесообразно ли отражать размеры тела с помощью ППТ?

Существует много формул для определения ППТ (что само по себе уже настораживает), все они эмпирические, некоторые из них весьма сложны и вычурны. Приведем некоторые из них (Sb — ППТ, m — масса тела, h — рост):

1) формула Дюбуа и Дюбуа [4]:

S_b[м²] = 0,007184 ∙ m[кг]^0,425 ∙ h[см]^0,725; (3.4.1)

2) формула Мостеллера [5]:

S_b[м²] = {(m[кг] ∙ h[см])/3600}^0,5; (3.4.2)

3) формула Хейкока [6]:

S_b[м²] = 0,024265 ∙ m[кг]^0,5378∙ h[см]^0,3964 (3.4.3)

4) формула Гехана и Джорджа [7]:

S_b[м²] = 0,0235 ∙ m[кг]^0,51456 ∙ h[см]0,⁴²²⁴⁶; (3.4.4)

5) формула Бойда [8]:

S_b[м²] = 0,0003207 ∙ m[г]^{(0,7285 – 0,0188∙lg m[г])} ∙ h[см]^0,3; (3.4.5)

6) формула Фудзимото [9]:

S_b[м²] = 0,008883 ∙ h[см]^0,663 ∙ m[кг]^0,444; (3.4.6)

7) формула Такахира [10]:

S_b[м²] = 0,007241 ∙ h[см]^0,725 ∙ m[кг]^0,425. (3.4.7)

Почти все эти формулы (кроме формул Бойда и Фудзимото) дают сходные результаты, иллюстрацию чего мы приводим в табл. 3.4.1.

Рассмотрим некоторую совокупность индивидов с одинаковой ППТ (для определенности — 2 м²), но разными ростом и массой тела. Проследим функцио–нальную зависимость массы тела от роста при его монотонном возрастании и такую же зависимость роста от массы тела при ее монотонном возрастании при условии постоянной ППТ (2 м²) и использовании формулы Дюбуа (рис. 3.4.1).

Легко увидеть, что одинаковую ППТ могут иметь индивиды, абсолютно не похожие друг на друга по антропометрическим показателям. Одну и ту же ППТ можно иметь как при массе тела 88 кг и росте 160 см, так и при массе тела 70 кг и росте 183 см. Вызывает большие сомнения то, что у этих людей должен быть одинаковый СВ (напомним, речь идет о состоянии покоя; если придется массу тела привести в состояние поступательного движения — ходьба, бег, то, естественно, больше энергии и, следовательно, кислорода придется затратить индивиду с большей массой, ибо кинетическая энергия равна mv²/2). В обоих примерах, которые встречаются в реальности, отличие массы тела от должной связано с недостатком/избытком мышечной/жировой ткани. Каково же их должное соотношение? На вопросы такого рода обычно отвечают после проведения обследования большого количества объектов, и среднее принимается за должное. На основе подобных обследований, кстати, был удачно придуман такой показатель, как индекс массы тела (ИМТ). Удачность выбора метода расчета ИМТ (m[кг]/h[м]²) заключается в том, что такая величина имеет свойство достаточно точно сохраняться в большом диапазоне должных значений роста и массы тела, однако на основании чего эти должные значения выбраны, не совсем ясно (почему-то предполагается, что масса тела (кг) должна численно равняться росту (см) минус 100). Но ведь, по большому счету, это дело вкуса! (Сравните, например, рубенсовских женщин с современными фотомоделями).

Разные ткани потребляют разное количество энергии (и кислорода) в единицу времени. В состоянии покоя четверть всей энергии потребляется мышцами, 1/5 — головным мозгом. Таким образом, при одинаковой ППТ или при одной и той же массе тела можно иметь разную массу мышечной ткани и, следовательно, разный основной обмен, и тогда нормирование СВ не только к ППТ, но и к массе тела выглядит проблематичным. Нормирование к массе тела имеет лишь то преимущество, что она легко измерима, тогда как точность вычисления ППТ вызывает сомнения.

Что касается нормировки давления крови, то этот показатель является нормированным по своей природе, так как отражает работу по перемещению единичного объема крови. Вопрос о нормировке ОПСС решается просто, если решен вопрос о нормировании СВ. Удельное периферическое сопротивление (УПСС — ρ) можно определить как

ρ = p / QI, (3.4.8)

где QI — сердечный индекс. Если СВ нормировать к ППТ, то единицей измерения УПСС является Н∙с∙м^‑3 (дин∙с∙см^‑3), или, с энергетической точки зрения, Дж∙с∙м^‑4 (эрг∙с∙см^‑4); м^‑4 = м^‑2∙м^‑2 можно рассматривать как две взаимно сопротивляющиеся площади соседних элементов движущейся крови.

Один из путей к упорядочиванию вопросов нормировки гемодинамических показателей видится нам в энергетическом подходе к изучению СК и кислородного бюджета, о чем пойдет речь далее.

Конфликт интересов. Автор заявляет об отсутствии какого-либо конфликта интересов при подготовке данной статьи.

Список литературы

1. Роджерс Э. Физика для любознательных. Т. 1. Материя, движение, сила: пер. с восьмого амер. изд. / Э. Роджерс; под. общ. ред. Л.А. Арцимовича. — Изд. 2-е, испр. — М.: Мир, 1969. — 474 с.

2. Михневич К.Г. О системе единиц измерения в медицине / К.Г. Михневич, Ю.В. Волкова, А.А. Хижняк // Медицина неотложных состояний. — 2017. — № 3(82). — С. 111-114.

3. Рашмер Р.Ф. Динамика сердечно-сосудистой системы: пер. с англ. М.А. Безносовой и Т.Е. Кузнецовой; под ред. Г.И. Косицкого. — М.: Медицина, 1981. — 600 с.

4. Du Bois D. A formula to estimate the approximate surface area if height and weight be known / D. Du Bois, E.F. Du Bois // Arch. Intern. Med. — 1916. — Vol. 17. — P. 863-871.

5. Mosteller R.D. Simplified calculation of body surface area / R.D. Mosteller // N. Engl. J. Med. — 1987. — Vol. 317. — P. 1098.

6. Haycock G.B. Geometric method for measuring body surface area: A height-weight formula validated in infants, children, and adults / G.B. Haycock, G.J. Schwarta, D.H. Wistosky // J. Pediatr. — 1978. — Vol. 93. — P. 62-66.

7. Gehan E.A. Estimation of human surface area from height and weight / E.A. Gehan, S.L. George // Cancer Chemother. Rep. (part 1). — 1970. — Vol. 54. — P. 225-235.

8. Boyd E. Experimental error inherent in measuring growing human body / E.Boyd // Am. J. Physiol. — 1930. — Vol. 13. — P. 389-432.

9. Fujimoto S. Studies on the physical surface area of Japanese. Calculation formulae in three stages over all ages / S. Fujimoto, T. Watanabe, A. Sakamoto, K. Yukawa, K. Morimoto // Nippon Eiseigaku Zasshi. — 1968. — Vol. 5. — P. 443-450.

10. Kouno T. Standardization of the Body Surface Area (BSA). Formula to Calculate the Dose of Anticancer Agents in Japan / T. Kouno, N. Katsumata, H. Mukai, M. Ando, T. Watanabe // Japanese Journal of Clinical Oncology. — 2003. — Vol. 33. — P. 309-313.